고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

Odds(아즈, 오즈)
Odds는 사건 A가 발생하지 않을 경우 대비 발생할 확률을 의미합니다.
Odds는 보통 도박에서 배당률을 결정할 때 이용하고 있습니다.
그리고 다음과 같이 정의 됩니다.

만약 사건 A의 성공 확률이 1일 경우 Odds는 무한대의 값을 갖게 됩니다.
성공 확률이 0일 경우 Odds는 0의 값을 갖습니다.
Odds를 이용하여 문제를 풀어보도록 하겠습니다.
예시 문제 1
항아리에 A 동전 두개와 B 동전 하나가 들어있습니다. 동전 A를 던졌을 때, 앞면이 나올 확률은 1/4, 동전 B를 던졌을 때, 앞면이 나올 확률은 3/4 라고 하겠습니다. 항아리에서 임의로 동전을 꺼내서 던지고 앞면이 나왔습니다. 이때 이 동전이 A일 확률은 얼마나 될까요?? P(A l heads)를 구하는 문제입니다.
이 문제는 Odds와 베이즈 정리 두 가지 방법으로 풀어볼 수 있습니다.
풀어보기 전에 각 사건을 정의하도록 하겠습니다.
사전 확률 : P(A) = 2/3, P(B) = 1/3
사전정보 조건부 확률 : P(heads l A) = 1/4, P(heads l B) = 3/4
(1) Odds를 이용한 풀이
앞면이 나왔을 때 동전이 A일 확률의 Odds는 다음과 같습니다.
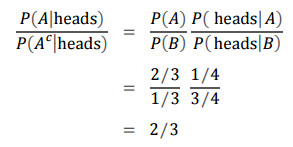
A일 확률과 A가 아닐 확률은 2:3의 비 이므로 A일 확률은 2/5가 됩니다.
(2) 베이즈 정리를 이용한 풀이
P(A l heads) = (P(A) * P(heads l A)) / (P(B) * P(heads l B) + P(A) * P(heads l A))
베이즈 정리 풀이에 대한 자세한 설명은 이전 포스팅에서 살펴보실 수 있습니다.
[확률론] 베이즈 정리(Bayes' Rule)
고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다. 김성범 교수님의 확률 강의는 정말 명강의라고 생각합니.
deep-learning-study.tistory.com
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 확률변수와 확률함수 (1) | 2021.02.01 |
|---|---|
| [확률론] 독립 사건 (0) | 2021.01.31 |
| [확률론] 베이즈 정리(Bayes' Rule) (0) | 2021.01.29 |
| [확률론] 조건부 확률과 확률의 곱셈 법칙 (1) | 2021.01.28 |
| [확률론] 확률의 공리와 기본 성질(Axioms and Basic Properties of Probability) (4) | 2021.01.25 |