고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

독립 사건(Independent Events)
이번 포스팅에서는 독립 사건에 대해 알아보도록 하겠습니다.
사건 A와 B가 독립이면 P(B l A) = P(B) 가 됩니다. 이것은 어떤 의미를 갖고 있을 까요??
사건 A가 발생하던 말던 사건 B의 확률이 동일하다는 것을 의미합니다.
그리고 이를 사건 A와 B가 독립(independent)이라고 합니다.
P(B l A) = P(B)에서 조건부확률을 교집합으로 표현해보도록 하겠습니다.
P(B l A) = P(BA) / P(A) = P(B) 가 됩니다.
이를 정리하면 P(AB) = P(A)P(B) 가 됩니다.
이처럼 사건 A,B가 독립일 경우 A와 B의 교집합은 각각의 곱으로 표현할 수 있습니다.
그리고 두 사건이 독립인지 확인하려면 P(AB) = P(A)(B) 를 성립하는지 확인하면 됩니다.
두 개의 사건이 아닌 n 개의 사건으로 확장할 수 있습니다.
P($A_1,A_2, ... ,A_n$) = P($A_1$)P($A_2$) ... P($A_n$)
독립 사건 예시 문제 1
독립 사건을 이용한 예시 문제를 풀어보도록 하겠습니다.
작은 마을에서 한 개의 소방차와 한 개의 응급차를 갖고 있습니다. 도움이 필요할 때 소방차를 이용할 수 있는 확률은 0.98이고, 응급차를 이용할 수 있는 확률은 0.92 입니다. 건물에 불이났을 때, 소방차와 응급차 둘 다 이용가능한 확률은 어떻게 될까요? 응급차와 소방차는 독립적으로 운행된다고 가정하겠습니다.
우선 각 확률을 정의해보겠습니다.
P(소방차) = 0.98
P(응급차) = 0.92
문제에서 묻는 것은 P(소방차 응급차) 입니다. 두 사건은 독립이므로 교집합은 다음과 같이 구할 수 있습니다.
P(소방차 응급차) = P(소방차) * P(응급차) = 0.996
독립 사건 예시 문제 2
2개의 주사위를 굴려 세 가지 사건이 생성되었습니다.
E1 = {합이 6}, E2 = {합이 7}. E3 = {첫 번째 주사위가 4}
(1) E1과 E2이 독립인 것을 증명하기
P(E1E2) = P(E1) * P(E2) 가 성립하는지 확인해 보면 됩니다.
P(E1E2) = 0
P(E1) * P(E2) = 5/36 * 6/36
성립하지 않으므로 E1과 E2는 종속입니다.
(2) E1과 E3은 독립인가요?
P(E1E3) = P(E1) * P(E3) 이 성립하면 두 사건은 독립이 됩니다.
P(E1E3) = 1/36, P(E1) * P(E3) = 5/36 * 6/36 이므로 성립하지 않습니다.
따라서 두 사건은 종속입니다.
(3) E2와 E3은 독립인가요?
P(E2E3) = 1/36
P(E2) * P(E3) = 1/36
P(E2E3) = P(E2) * P(E3) 이 성립하므로 두 사건은 독립입니다.
독립 사건의 성질
사건 E와 F가 독립이면 E와 $F^c$도 독립입니다.
증명
사건 E와 F가 독립이라고 가정하겠습니다. 따라서 E = EF $\cup$ E$F^c$이고, EF와 E$F^c$는 상호 배반입니다. 따라서 식을 다음과 같이 정리할 수 있습니다.

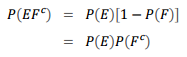
따라서 E와 F가 독립이면, E가 발생할 확률은 F가 발생했는지 안했는지에 대한 정보에 의해 변경되지 않습니다.
사건이 3개인 경우 독립 사건
다음을 만족할 때, 사건 E, F, G는 독립입니다.
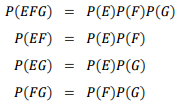
그리고 만약 사건 E, F, G가 독립이면 E는 F와 G로 형성된 어떤 사건들과도 독립입니다.
예를 들어 E와 F $\cup$ G가 독립인지 확인하겠습니다.

이를 통해 사건 E와 F $\cup$ G는 독립이라는 것을 확인할 수 있습니다.
몇 가지 예시 문제를 풀어보도록 하겠습니다.
예시 문제 1
독립 시행이 연속적으로 무한번 시행됬다고 하겠습니다. 각 시행 결과는 성공 확률 p, 실패 확률 1-p입니다.
(1) n번 시행해서 적어도 1번 이상 성공할 확률
n번 시행해서 모두 실패할 확률을 1에서 빼주면 구할 수 있습니다.
1 - P(all n fail) = 1 - $(1-p)^n
(2) n번 시행해서 정확히 k번 성공이 발생할 확률
이 확률을 구할려면 조합의 개념이 필요합니다.
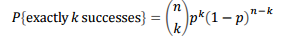
n번 중 k번 성공하고 n-k번은 실패할 확률입니다.
(3) 모든 시행이 성공할 확률
각 시행이 성공할 확률은 p입니다 따라서 모든 시행이 성공할 확률은 $p^n$이 됩니다.
이를 확장하면 다음과 같습니다.

예시 문제 2
다음과 같이 n개의 분리된 요소로 구성된 시스템을 병렬 시스템이라고 합니다. 만약 하나의 요소라도 작동한다면 병렬 시스템은 작동하게 됩니다. 이러한 시스템은 각 요소 i가 다른 요소들과 독립입니다. 각 요소가 작동할 확률을 p라고 할때, 시스템이 작동할 확률은 어떻게 될까요?
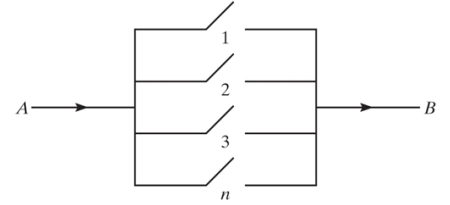
1에서 모든 요소가 작동하지 않을 확률을 빼주면 구할 수 있습니다.
1 - P(all n fail) = 1 - {$(1-p)^n$}
예시 문제 3
두 쌍의 주사위로 구성된 독립된 시행이 수행되었습니다. 두 주사위의 합이 5가 합이 7인 경우 전에 발생할 확률은 어떻게 될까요?
우선 각 사건의 확률을 정의합니다.
P(S = 5) = 4/36
P(S = 7) = 6/36
합이 5와 7이 발생하지 않을 확률을 정의합니다. 이는 1- P(S=5 $\cup$ S=7)로 구할 수 있습니다.
1-P(S=5 $\cup$ S=7) = 1 - (10/36) = 26/36
첫 번째 시행에서 5가 나올 확률
P(E1) = 4/36
이전 시행에서 5와 7이 나오지 않고 두 번째 시행에서 5가 나올 확률
P(E2) = 26/36 * 4/36
이전 시행에서 5와 7이 나오지 않고 세 번째 시행에서 5가 나올 확률
P(E3) = 26/36 * 26/36 * 4/36
이를 확장하면 다음과 같습니다.
P(En) = $(26/36)^n$ * 4/36 = 2/5
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 기댓값(Expectation) (1) | 2021.02.05 |
|---|---|
| [확률론] 확률변수와 확률함수 (1) | 2021.02.01 |
| [확률론] Odds(오즈, 아즈) (0) | 2021.01.29 |
| [확률론] 베이즈 정리(Bayes' Rule) (0) | 2021.01.29 |
| [확률론] 조건부 확률과 확률의 곱셈 법칙 (1) | 2021.01.28 |