고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

집합 연산(Set Operation)
집합의 세 가지 연산에 대해 알아보도록 하겠습니다.
1. 교집합(intersection)
표본 공간에서 두 사건 E와 F에 대하여 새로운 사건 EF를 정의하고, 이를 E와 F의 교집합이라고 부르겠습니다.
즉, EF(E$\cap$F)는 사건 E와 F가 동시에 발생하는 것을 의미합니다.
예를 들어, 동전을 두 번 던질 때 사건 E는 적어도 1번 이상 앞면이 나올 사건(E = {(h,h), (h,t), (t,h)})이고, 사건 F는 적어도 1번 이상 뒷면이 나올 사건(F = {(t,t), (t,h), (h,t)})이라고 할 때, E와 F의 교집합 EF는 {(h,t), (t,h)}가 됩니다.
교집합을 벤다이어 그램으로 나타내면 다음과 같습니다.

만약 사건 E와 F의 교집합이 존재하지 않으면 상호 배타(Mutually Exclusive)라고 합니다.
E $\cap$ F = AB = $\phi$
2. 합집합(Union)
표본 공간 S에 있는 사건 E와 F의 합집합은 E와 F가 둘 다 발생한 것을 의미하고 E$\cup$F로 표시합니다.
예를 들어 사건 E는 전구의 수명이 200시간 미만일 사건(E = {0 <= x < 200})이고, 사건 F는 전구의 수명이 5시간 이상 500 미만(F = {5 <= x <500})일 때, E와 F의 합집합은 {0 <= x < 500}이 됩니다.
합집합을 벤다이어 그램으로 다음과 같이 나타낼 수 있습니다.
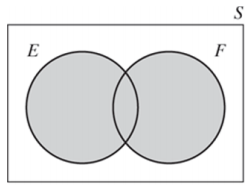
3. 여집합(Complement)
마지막으로 알아볼 집합 연산은 여집합 입니다.
사건 E의 여집합은 표본 공간 S에서 사건 E를 뺀 것을 의미합니다. 그리고 $E^c$로 표시합니다.
사건 E가 전구의 수명이 200시간 미만일 사건(E = {0 <= x < 200}) 일 때, E의 여집합은 {200 <= x}가 됩니다.
벤다이어 그램으로 다음과 같이 나타낼 수 있습니다.

세 가지 집합 연산에 대해 알아보았습니다. 다음에는 집합의 법칙에 대해 알아보도록 하겠습니다.
집합의 법칙(Laws of Set Operation)
- 교환 법칙(Commutative law)
E $\cup$ F = F $\cup$ F, EF = FE
- 결합 법칙(Associative law)
(E $\cup$ F) $\cup$ G = E $\cup$ (F $\cup$ G), (EF)G = E(FG)
괄호 안의 순서를 바꿀 수 있습니다.
- 분배 법칙(Distribution law)
(E $\cup$ F)G = (EG) $\cup$ (FG)
(EF) $\cup$ G = (E $\cup$ G)(F $\cup$ G)
- 드모르간의 법칙(De Morgan's law)

위 수식을 확장하면 아래와 같이 됩니다.

'수학 > 확률론' 카테고리의 다른 글
| [확률론] 베이즈 정리(Bayes' Rule) (0) | 2021.01.29 |
|---|---|
| [확률론] 조건부 확률과 확률의 곱셈 법칙 (1) | 2021.01.28 |
| [확률론] 확률의 공리와 기본 성질(Axioms and Basic Properties of Probability) (4) | 2021.01.25 |
| [확률론] 표본 공간과 사건(Sample Space and Events) (0) | 2021.01.25 |
| [확률론] 1. 순열과 조합 (4) | 2021.01.24 |