고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

실험(Experiment)
실험은 데이터 집합을 생성하는 과정을 의미합니다.
예시 : 동전 던지기, 주사위 굴리기, 슈퍼마켓에 있는 손님들의 수 세기
Counting의 기본 원리
2개의 실험을 수행한다고 가정하겠습니다.
첫 번째 실험이 m개의 결과를 갖고 있고, m개의 첫 번째 실험의 각 결과에 대하여 두 번째 실험은 n개의 결과를 갖습니다.
그러면 두 실험의 모든 가능한 결과는 얼마나 많을까요??

모든 가능한 결과의 집합은 m개의 행과 n개의 열로 이루어져 있습니다. 따라서 총 mn개의 결과가 도출됩니다.
counting의 수학적인 이론은 공식적으로 조합 분석(combinatorial analysis)라고 합니다.
일반화된 Counting의 기본 원리
Counting의 기본 원리는 곱의 법칙(Multiplication rule)로 나타낼 수 잇습니다.
- 가능한 결과의 수 = $n_1,n_2,...n_k$
- 동전을 3번 던졌을 때 결과의 수 = 2 $\cdot$ 2$\cdot$ 2 = 8
예시
1. 부동산 개발업자가 다음의 조건을 제시 합니다.
- 외부 스타일: 4개
- 바닥 종류: 3개
이때, 가능한 집의 수 = 4 $\cdot$ 3 = 12
2. 각 학년(1학년, 2학년, 3학년, 4학년)에서 하나씩 뽑아, 4명의 학생으로 위원회를 구성하려고 합니다. 얼마나 많은 위원회를 만들 수 있을 까요?
- 1학년 10명
- 2학년 22명
- 3학년 13명
- 4학년 2명
가능한 위원회 수 = 10 x 22 x 13 x 2 = 5,720
순열(Permutation)
순열은 집합에서 모든 배열 또는 부분 배열입니다. 따라서 순서가 고려되어야 합니다.
다른 말로 하면, 물체를 나열하는 순서는 구분됩니다.
n개의 물건을 갖고 있다고 가정해보겠습니다. n개의 물건의 서로 다른 순열은 n!개 입니다.

예시
1. 수학책 4개, 화학책 3개, 역사책 2개, 언어책 1개 총 10개의 책을 갖고 있습니다. 이 책들을 4층의 책장에 과목 별로 구분하여 정리하고 싶을 때 몇 가지 방법이 가능할까요?
- 수학 책의 순서 = 4! = 24
- 화학 책의 순서 = 3! = 6
- 역사 책의 순서 = 2! = 2
- 언어 책의 순서 = 1! = 1
- 과목의 순서 4! = 24
- 순서의 모든 수 = 4! x 4! x 3! x 2! x 1! = 6912
중복 순열(Nondistinguishable permutations)
n개의 물건에서 $n_1$개가 하나의 동일한 종류이고 $n_2$가 두 번째 동일한 종류, ... , $n_k$가 k 번째 동일한 종류일 때, 중복 순열은 다음과 같이 표현할 수 있습니다.

예시 문제
10개의 야구 선수들 중에, 1학년 1명, 2학년 2명, 3학년 4명, 4학년 3명이 있습니다. 이들이 각 학년이 구별되어 한 줄로 나열되는 경우의 수는 어떻게 될까요?
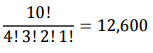
조합(Combiantion)
A,B,C,D,E 5개에서 3개를 선택하는 경우를 생각해보겠습니다. 첫 번째 알파벳을 선택하는 경우는 5가지, 다음 알파벳을 선택하는 경우는 4가지, 마지막 알파벳을 선택하는 경우는 3가지 입니다. 즉, 순서를 고려한 결과는 5 x 4 x 3이 됩니다. 하지만 순서를 고려하지 않게 된다면 ABC, ACB, BAC, BCA, CAB, CBA는 한가지 경우의수가 됩니다. 이 경우에 어떻게 구해야 할까요?? 이처럼 순서를 고려하지 않고 선택하는 것을 조합이라고 부르며 식은 다음과 같이 표현할 수 있습니다.

즉, 조합은 n개에서 r개를 선택할 때, 순서를 고려하지 않고 선택하는 것을 의미합니다.
그리고 기호로는 다음과 같이 나타냅니다.
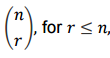
예시 문제
20명의 사람들 중에서 3명을 선택해 위원회를 구성하는 경우의 수는 어떻게 될까요? 이는 조합으로 풀 수 있습니다.

이항 정리(Binomial Theorem)
이항 정리를 조합을 이용하여 나타낼 수 있습니다.

여기서,
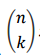
를 이항 계수(Binomial coefficient)라고 합니다.
예시 문제

를 조합으로 확장하는 문제입니다.
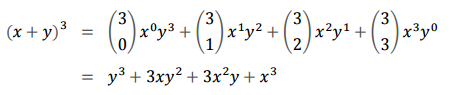
다항 계수(Multinomial Coefficients)
작은 도시에 10명의 경찰로 구성된 경찰서가 있다고 가정해보겠습니다. 만약에 5명이 거리를 순찰해야하고 2명이 역에서 근무를 해야하고 3명이 역에 남아있어야 한다면, 10명의 경찰을 3개의 그룹으로 나누는 방법은 몇개가 있을 까요??
이는 다음과 같이 구할 수 있습니다.

이처럼 $n_1$ + $n_2$ + ... + $n_r$ = n이 되고 n을 r개의 그룹으로 나눌 때 다음과 같은 식으로 구할 수 있습니다.
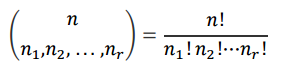
이를 다항 계수라고 합니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 베이즈 정리(Bayes' Rule) (0) | 2021.01.29 |
|---|---|
| [확률론] 조건부 확률과 확률의 곱셈 법칙 (1) | 2021.01.28 |
| [확률론] 확률의 공리와 기본 성질(Axioms and Basic Properties of Probability) (4) | 2021.01.25 |
| [확률론] 집합 연산(Set Operation)과 집합 연산의 법칙(Laws of Set Operation) (1) | 2021.01.25 |
| [확률론] 표본 공간과 사건(Sample Space and Events) (0) | 2021.01.25 |