고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

분산(Variance)
확률 변수 X가 주어졌을 때, X의 분포를 요약할 수 있는 모수가 있으면 편리할 것입니다. X의 분포를 요약하는 모수는 E[X] 기대값이 있습니다. 하지만 E[X]는 X의 가중 평균을 의미하기 때문에 편차, 흩어짐 등을 나타내지 않습니다.
예를 들어, 확률 변수 W, Y, Z가 다음과 같은 확률 질량 함수를 갖고 있다고 해보겠습니다.

이 세개의 확률 변수의 기대값은 0으로 동일합니다.
그리고 Y는 W보다 흩어짐이 크고, Z가 Y보다 흩어짐이 크다는 것을 생각해볼 수 있습니다.
확률 변수의 값이 평균값과 얼마나 떨어져 있는지 편차를 계산하기 위해서 E[lX-ul]를 계산해볼 수 있습니다. 여기서 u는 기대값입니다. 하지만 이 방법은 수학적으로 불편합니다.
따라서 다음과 같이 분산을 정의하고 분포의 흩어짐을 나타내는 파라미터로 사용합니다.

여기서 u는 E[X]입니다.
분산은 얼마나 흩어져있는지를 의미하고 평균값으로부터 얼만큼의 편차가 있는지를 나타냅니다.
분산은 음수값을 가질 수 없습니다.
즉, 정리하면 분산은 기대값을 기점으로 얼마나 떨어져있는지 제곱의 스케일로 표현한 척도입니다.
분산을 다른 식으로 나타내면 다음과 같습니다.

즉, 분산은 다음과 같이 됩니다.
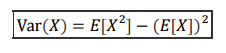
분산은 X 제곱의 기대값에서 X의 기대값을 빼주어 계산할 수 있습니다.
예시 문제 1
확률 변수 X를 주사위를 굴렸을 때 나오는 결과값이라고 정의하겠습니다. Var(X)를 구하는 문제입니다.
확률 변수 X가 가질 수 있는 값은 X = {1, 2, 3, 4, 5, 6}이 됩니다.
각각의 확률은 1/6이 됩니다.
이제 분산을 구해보겠습니다.
E[X] = 1 * 1/6 + 2 * 1/6 + 3 * 1/6 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6 = 7/2


분산은 음수의 값을 갖지 않습니다. 따라서 X의 제곱의 기대값이 X의 기대값의 제곱보다 항상 크다고 생각해볼 수 있습니다.

분산의 성질
c와 b는 상수입니다.
(1) Var(c) = 0
(2) Var(cX) = $c^2$Var(X)
(3) Var(aX + b) = $a^2$Var(X)
예시 문제 1
확률 변수 X를 두 개의 동전을 던졌을 때 앞면의 수로 정의하겠습니다.
X가 가질 수 있는 값은 X = {0, 1, 2} 이고 각각의 확률은 P(0) = 1/4, P(1) = 1/2, P(2) = 1/4 입니다.
Var(X) = E[X^2] - (E[X])^2 = 3/2 - 1 = 1/2
일때, Var(-4X + 3)을 구하는 문제입니다.
Var(-4X + 3) = 16Var(X) = 8
표준 편차(Standard Deviation)
표준 편차는 분산의 제곱근을 취한 것입니다.
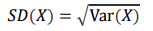
이 표준편차에 대해서는 추후에 자세히 설명하도록 하겠습니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 이산형 확률분포 - 이항분포 (0) | 2021.02.08 |
|---|---|
| [확률론] 이산형 확률분포 - 베르누이 분포 (3) | 2021.02.07 |
| [확률론] 기댓값(Expectation) (1) | 2021.02.05 |
| [확률론] 확률변수와 확률함수 (1) | 2021.02.01 |
| [확률론] 독립 사건 (0) | 2021.01.31 |