반응형
고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

초기하 분포(Hypergeometric Distribution)
m개 흰색 공, N - m개 검은색 공으로 구성된 N개의 공을 포함하고 있는 항아리에서 비복원 추출로 n개 공을 꺼낸다고 가정하겠습니다.
확률 변수 X는 흰색 공이 뽑힌 수로 정의합니다.
초기하 분포의 확률질량함수는 다음과 같습니다.

파라미터는 n: 샘플링 수, N: 공의 수, m: 흰색 공의 수 3가지를 갖습니다.
그리고 초기하 분포는 품질에서 불량이 몇개 인지 파악하기 위해 많이 쓰입니다.
초기하 분포의 파라미터
초기하 분포는 N, n, m 3가지 파라미터를 갖으며 이 파라미터는 분포의 모양을 결정합니다.
N: 샘플링 수
n: 공의 수
m : 흰색 공의 수
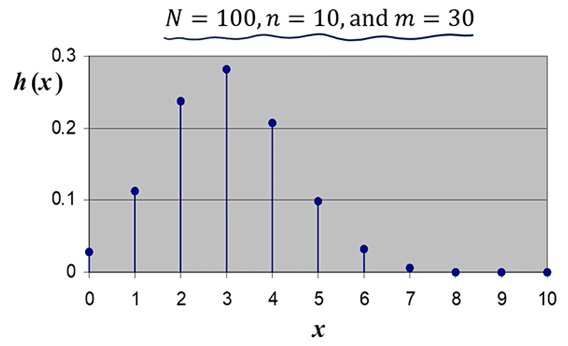
초기하 분포의 기대값과 분산
기대값과 분산은 파라미터의 함수입니다.


초기하 분포 예시 문제
나사가 10개 들어있는 박스를 구매하려고 합니다. 3개의 나사를 임의로 선택해서 결함이 없으면 구매합니다. 10개의 나사 중 4개가 결함이 있는 나사일 확률은 0.3, 1개가 결함이 있는 나사일 확률은 0.7 입니다. 나사 박스를 구매할 확률은 어떻게 될까요?
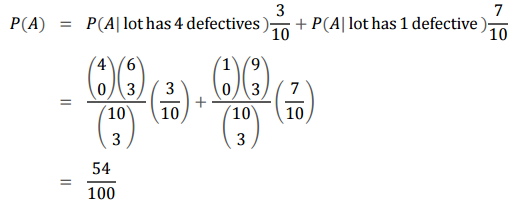
여태까지 공부한 용어들을 정리해보도록 하겠습니다.
- 실험(Experient): 데이터를 생성하는 모든 과정
- 표본 공간(Sample Space): 실험으로부터 얻은 모든 결과값들의 집합
- 확률 변수(Random Variable): 표본 공간의 요소들을 실수로 대응시키는 함수
- 확률 함수(Probability Function): 확률 값을 생성하는 함수
- 확률 분포(Probability Distribution): 확률 함수로부터 나온 확률 값들의 패턴
반응형
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 연속형 확률분포 - 정규 분포(Normal Distribution) (0) | 2021.03.05 |
|---|---|
| [확률론] 연속형 확률 분포 - 일양 분포(uniform distribution) (0) | 2021.03.04 |
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |
| [확률론] 이산형 확률분포 - 기하분포 (2) | 2021.02.12 |
| [확률론] 이산형 확률분포 - 포아송 분포 (0) | 2021.02.10 |