고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

정규 분포(Normal Distribution)
정규분포는 가우시안 분포(Gaussian Distribution)으로 부르기도 합니다.
확률 변수 X가 정규 확률 변수거나 정규 분포를 따를 때, 확률 밀도 함수(pdf)는 다음과 같습니다.

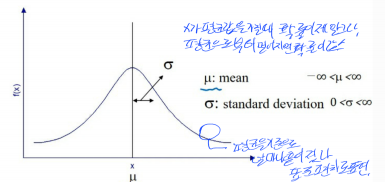
모수(parameter)는 $\mu$(평균), $\sigma^2$(분산) 입니다.
모수는 확률 분포의 모양을 결정하는 중요한 수입니다.
$\mu$ = 0, $\sigma$ =1 일때, 정규 분포는 다음과 같습니다.
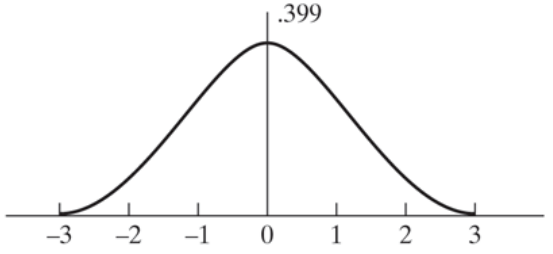
위 분포에서 모수가 바뀌게 되면 분포의 위치와 모양이 변경됩니다.
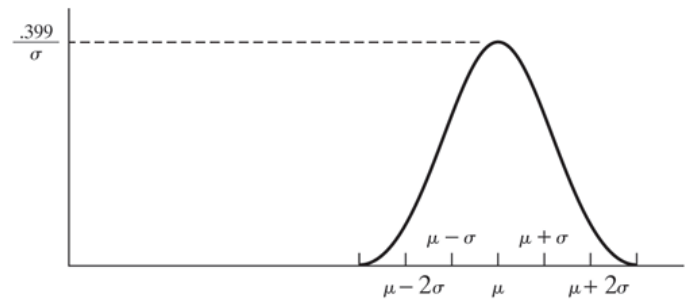
정규 분포의 특성(Characteristics of Normal Distribution)
- 평균을 기준으로 대칭입니다.(ball-shape curve)
- X=$\mu$일 때, 확률이 최대입니다.
- 전체 면적은 1입니다.(확률 분포의 특성)
모수에 따른 정규 분포
모수는 확률 분포의 모양을 결정하는 중요한 수입니다. 정규 분포의 모수인 평균과 표준편차에 따라 분포의 모양이 결정됩니다.

정규 분포의 기대값과 분산
기대값과 분산은 다음과 같습니다.

표준 정규 분포(Standard Normal Distribution)
표준 정규 분포는 정규 분포를 따르는데, 모수가 평균=0, 분산=1인 분포입니다.
정규 분포는 새로운 확률 변수 Z를 다음과 같이 정의하여 사용합니다. 정규 확률 변수에 평균을 뺴주고 표준편차를 나눠준 것입니다.

Z~N(0,1)로 표기하고, N은 normal distribution을 의미합니다. Z는 평균=0, 분산=1인 정규분포를 따른다는 의미입니다.
표준 정규 분포를 사용하는 이유는 정규 분포의 cfd를 구할 때, 적분을 해야합니다. 이 과정이 번거로우므로 정규 분포를 표준 정규 분포로 바꾼뒤에 표준 정규 분포표를 보고 cdf를 쉽게 구할 수 있습니다.
정규 확률 분포의 확률 밀도 함수(pdf)는 다음과 같습니다.

Z의 cdf는 표로 정리되어 있습니다. 그리고 표준 정규 분포의 cdf를 $\phi$로 표기합니다.

표준 정규 분포의 cdf
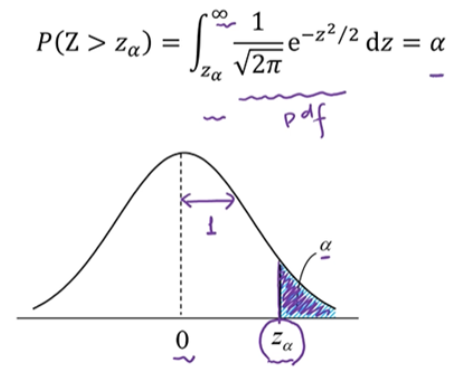
표준 정규 분포가 $Z_a$보다 클 확률은 a입니다. 이 a는 표준 정규 분포표 or Z 테이블에 정리되어 있습니다.
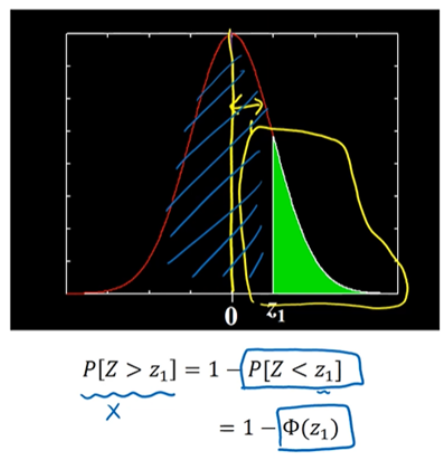
표준 정규 분포가 $z_1$보다 클 확률은 위와 같은 방법을 이용합니다.

$-z_1$보다 작을 확률은 1에서 $z_1$보다 작을 확률을 빼주면 됩니다. 표준정규분포는 대칭이기 때문에 가능합니다.
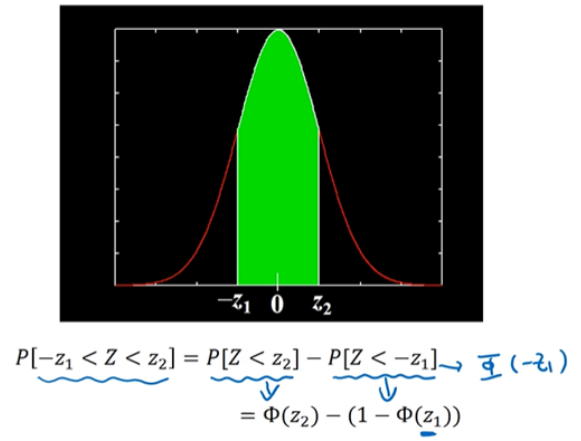
사이 확률은 $z_2$에서 -$z_1$을 빼주면 됩니다.
이항 분포를 정규 분포로 근사화(Normal Approximation of the Binomial Distribution)
특정 조건에서 이항 분포를 정규 분포로 근사화할 수 있습니다.
이항 분포는 이산형 확률 변수를 취하므로 계산이 복잡합니다. 이를 연속형으로 바꾸면 계산이 편리합니다. 이산형 분포의 cdf를 구할 때, 정규 분포로 근사화해서 구하는 것입니다. 근사화는 특정 조건에서만 잘 작동합니다.
이항 분포의 모수는 n, p입니다. 이 n,p가 특정 조건을 만족할 시에 근사화가 잘 작동합니다.
1) n이 커야합니다.
2) p는 0이나 1에 너무 가깝지 않아야 합니다.

이항 분포를 정규 분포로 근사화했을 때, 모수는 평균 = np, 분산 = np(1-p) 입니다.
이항 분포를 정규 분포로 근사화 한뒤에, 표준 정규 분포로 바꾸어서 편리하게 cdf를 구할 수 있습니다.
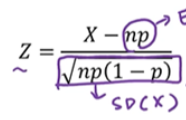

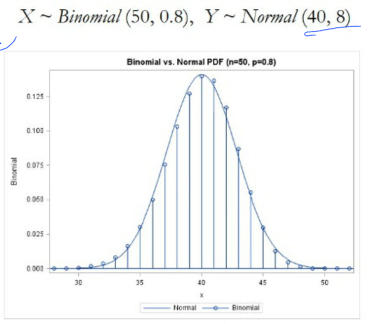
n에 따른 이항 분포의 모양입니다. n이 커질수록 모양이 정규 분포와 가까워 집니다.

연속성 수정(continuity correction)
이항분포를 정규분포로 보다 정확하게 근사하게끔 해주는 값입니다.
이산형을 연속형으로 일치시키긴 쉽지 않습니다. 이를 잘 근사화하기 위해 -0.5, +0.5를 해주면 근사가 잘 됩니다. 0.5는 경험적으로 나온 수치입니다. 그리고 이를 연속성 수정이라고 합니다.


예시 문제
동전을 40번 던졌을 때, 앞면이 20개 나올 확률을 구하는 문제입니다. 이항 분포를 정규분포로 근사화해서 풀어보고, 단순히 이항분포로도 풀어보겠습니다.
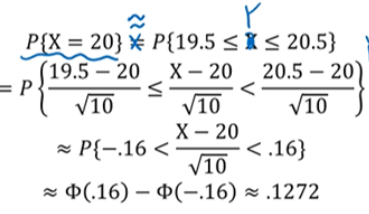
연속성 수정을 한뒤에 정규분포로 근사화했을 때, 0.1272가 나왔습니다.

단순히 이항 분포로 풀었을 때, 0.1254가 나왔습니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 연속형 확률분포 - 감마 분포(Gamma Distribution) (1) | 2021.03.07 |
|---|---|
| [확률론] 연속형 확률분포 - 지수 분포(Exponential distribution) (0) | 2021.03.06 |
| [확률론] 연속형 확률 분포 - 일양 분포(uniform distribution) (0) | 2021.03.04 |
| [확률론] 이산형 확률분포 - 초기하 분포 (1) | 2021.02.14 |
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |