고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

감마분포(Gamma Distribution)
감마분포는 지수분포의 일반화된 형태입니다. 두 개이상의 지수분포가 합쳐지면 감마분포가 됩니다.
확률 변수 X는 k개의 이벤트가 발생할 때까지 걸리는 시간으로 정의합니다. 그리고 시간과 관련되어 있으므로 항상 0보다 큰 값을 갖습니다.
감마분포의 확률밀도함수(pdf)는 다음과 같습니다. 모수(파라미터)는 람다와 알파를 지닙니다.

감마 확률밀도함수는 감마함수를 정의하여 사용합니다.

감마함수의 특성은 다음과 같습니다.



감마분포의 모수
모수는 확률분포의 모양을 결정하는 중요한 수입니다.
감마분포는 알파와 감마, 두 가지 모수가 존재하며, 알파를 형상모수(shape parameter), 람다를 척도모수(scale parameter)이라고 합니다.
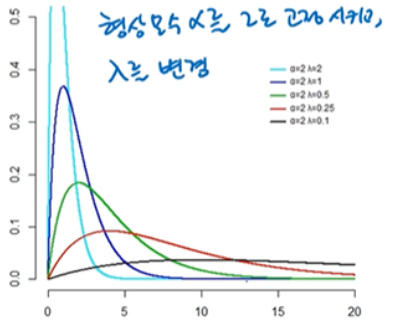
아래 그림은 척도모수 람다를 1로 고정하고 알파를 변경한 것입니다.

형상모수 알파를 1로 고정하고 람다를 변경한 그림입니다.
감마분포의 기대값과 분산
기대값과 분산은 모수로 정의된 함수입니다. 감마분포의 기대값과 분산은 다음과 같습니다.

감마분포의 특성
감마분포는 지수분포의 일반화된 형태입니다.
지수분포는 모수 람다를 갖고 있습니다.
람다는 단위 시간당 발생하는 이벤트의 평균횟수 입니다.
감마분포에서 알파가 1인 경우에 지수분포와 같습니다.
즉, 지수분포는 감마분포에서 알파가 1인 것에 해당합니다.
지수분포를 따르는 확률변수가 알파개 있다고 해보겠습니다. ($X_1, ... ,X_{\alpha}$)
이 확률변수를 모두 다 더하면 감마분포가 됩니다.
즉, 감마분포는 지수분포의 합입니다.
지수분포를 따르는 확률변수 X가 5개가 있고, 각 확률변수는 iid(독립적이고 균등한 분포)를 따른다고 하면, 이 확률변수의 합은 알파가 5인 감마분포로 나타낼 수 있습니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 연속형 확률분포 - 지수 분포(Exponential distribution) (0) | 2021.03.06 |
|---|---|
| [확률론] 연속형 확률분포 - 정규 분포(Normal Distribution) (0) | 2021.03.05 |
| [확률론] 연속형 확률 분포 - 일양 분포(uniform distribution) (0) | 2021.03.04 |
| [확률론] 이산형 확률분포 - 초기하 분포 (1) | 2021.02.14 |
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |