반응형
고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

일양 분포(Uniform Distribution)
일양 분포는 확률 변수 X가 구간 $\alpha, \beta$에서 균일한 확률을 지니고 있습니다.
확률 밀도 함수는 다음과 같이 정의합니다.
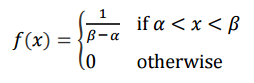

연속형 확률 분포의 총합(면적)은 1이 되어야 합니다.
구건 $\alpha, \beta$ 사이에 일정한 확률을 갖고, 면적이 1이 되야 하므로 확률은 1/($\beta - \alpha$가 됩니다.
일양 분포의 cdf는 세 가지 구간으로 나눠서 살펴볼 수 있습니다.


일양 분포의 기대값과 분산
기대값과 분산은 다음과 같이 정의합니다.
기대값

기대값은 구간의 평균값으로 생각해볼 수 있습니다.
분산은 $E[x^2] - (E[x])^2$ 로 구합니다.

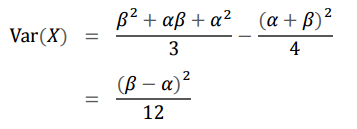
일양 분포 예시 문제
버스가 7시부터 15분 간격으로 도착합니다.(7, 7:15, 7:30, 7:45, ... ). 만약 승객이 7시부터 7시30분까지 균일한 분포로 버스정류장에 도착할 때, 5분 이하로 기다릴 확률은 어떻게 될까요??
확률 변수 X는 5분 미만 기다릴 확률로 정의합니다.
그리고, 확률은 구간 사이 동일한 값을 가져야 하므로 1/30으로 정의할 수 있습니다.
버스가 7시 15분, 7시 30분에 도착하므로 승객이 7시10분, 7시25분에 도착하면 5분 미만 기다리게 됩니다.

반응형
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 연속형 확률분포 - 지수 분포(Exponential distribution) (0) | 2021.03.06 |
|---|---|
| [확률론] 연속형 확률분포 - 정규 분포(Normal Distribution) (0) | 2021.03.05 |
| [확률론] 이산형 확률분포 - 초기하 분포 (1) | 2021.02.14 |
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |
| [확률론] 이산형 확률분포 - 기하분포 (2) | 2021.02.12 |