고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

지수 분포(Exponential Distribution)
정규분포 다음으로 많이 쓰이는 지수분포입니다. 지수분포는 항상 시간을 떠올려야 합니다. 지수 분포는 이벤트 사이의 시간(이벤트 A와 이벤트 B 사이에 걸린 시간)을 모델링하는데 많이 이용합니다. 각 이벤트는 포아송분포에 의해서 생성됩니다.
지수 분포의 모수(parameter)는 람다($\lambda$) 입니다. 람다는 단위 시간동안 평균 이벤트 발생횟수를 의미합니다. 포아송 분포의 모수와 동일합니다. 포아송 분포와 지수 분포는 밀접한 관계가 존재합니다. 이 둘의 관계를 알아보기 전에 지수분포에 대해 알아보겠습니다.
지수 분포의 pdf와 cdf는 다음과 같습니다.


지수분포는 주로 cdf를 이용합니다.
지수분포의 예로는 1. 서비스 기관에 두 고객이 도착했는데, 그 고객들의 도착과 도착 사이에 걸리는 시간. 2. 전자기기 부품의 고장 간격 시간, 다음 고장이 일어날때 까지 걸리는 시간. 을 모델링할 때 주로 이용합니다.
지수 분포의 모수(The parameter if the exponential distribution)
모수는 분포의 모양을 결정하는 중요한 수입니다.
지수확률 변수 X는 0보다 큰 실수값을 갖습니다. 이 모든 것을 확률로 바꾸려면 확률 함수가 필요합니다. 모수는 람다($\lambda$)입니다. 람다는 단위 시간당 이벤트의 평균 발생 횟수를 의미합니다.
그리고 이 람다는 지수 분포의 모양을 결정하는 모수입니다.

평균과 분산(Mean and Variance)
지수 분포의 평균과 분산입니다.
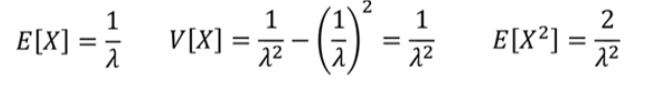
지수 분포 예시 문제
한 사람이 통화하는데 걸리는 시간은 1/10 입니다. 어떤 사람이 공중전화 앞에 도착했습니다. 이 사람이 전화를 하기 위해서 얼마나 기다려야하는지 확률을 계산하겠습니다. 기다리는 사이 시간이 지수분포를 따릅니다.
확률 변수 X = 기다리는 시간 으로 정의합니다.
모수인 람다는 1/10 입니다.
a) 10분이상 기다려야 할 확률

b) 10분이상 20분이하 기다릴 확률
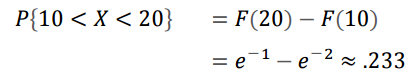
기억상실 특성(Memoryless Property)
지수분포의 중요한 특성인 기억상실 특성(Memoryless Property)입니다.
과거의 조건이 현재 확률에 영향을 미치지 않는 특성입니다. 과거를 기억하지 못하므로 기억상실 특성이라고 부릅니다.
(1) X가 t시간 이상 진행되었는데(조건부 확률), 추가로 s시간 진행할 확률은
(2) X가 s시간 이상 갈 확률과 같습니다.
결국 t가 의미가 없는 것입니다.
어떤 기계 수명이 확률변수 x입니다. t시간 작동하는 기계가 있습니다.
t시간 작동했는데 추가적으로 s시간 더 작용할 확률은 무엇일까요?
과거 t시간 작동했던 안했던 s시간 더 작동했을 확률과 같습니다.
즉, 조건부확률을 무시하는 것입니다.
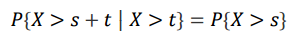
조건 X>t가 무시됩니다.
X가 s + t 시간 이상 작동할 확률은 s시간 이상 작동할 확률과 t시간 이상 작동할 확률의 곱으로 계산할 수 있습니다.
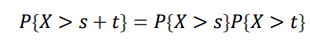
위 특성 덕분에 문제를 풀 때, 쉽게 풀리는 문제가 많습니다. 현실은 지나간 t시간이 중요할 수 있지만 지수분포는 지나간 t시간을 고려하지 않으므로 쉽게 풀 수 있는 것입니다.
기억상실 특성 예시 문제
자동차 배터리가 100퍼센트 소진될때 까지의 수명은 10,000 km입니다. 어떤 사람이 5,000 km 여행하고 싶은데 배터리를 교체하지 않고 여행을 다녀올 확률은 어떻게 될까요?
배터리는 이미 기존에 소모한 수명 T가 존재합니다. 여기에 추가적으로 5,000km 더 작동할 확률을 계산하는 것입니다. 기억상실 특성덕분에 T는 고려하지 않습니다.
확률변수는 베터리가 소진할 때 까지 걸리는 시간 X > 5,000 으로 정의합니다.
람다는 1/10,000 입니다.

지수 분포와 포아송 분포의 관계
포아송 분포는 단위 시간 이벤트가 몇번 발생했는지에 대한 확률입니다. 이벤트의 수에 관심이 있습니다.
지수 분포는 이벤트와 이벤트 사이 간격의 확률을 계산합니다. 이벤트 사이의 시간에 관심이 있습니다. 그리고, 각 이벤트는 포아송 분포에 의해 발생됩니다.
이 둘을 그림으로 나타내면 다음과 같습니다.
포아송분포 : t시간 동안 발생하는 평균 이벤트의 수

지수분포 : 이벤트와 이벤트 사이의 시간

'수학 > 확률론' 카테고리의 다른 글
| [확률론] 연속형 확률분포 - 감마 분포(Gamma Distribution) (1) | 2021.03.07 |
|---|---|
| [확률론] 연속형 확률분포 - 정규 분포(Normal Distribution) (0) | 2021.03.05 |
| [확률론] 연속형 확률 분포 - 일양 분포(uniform distribution) (0) | 2021.03.04 |
| [확률론] 이산형 확률분포 - 초기하 분포 (1) | 2021.02.14 |
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |