딥러닝 공부방

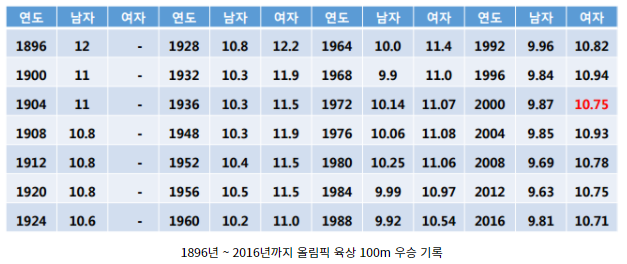
이미지 스티칭 - Image Stitching 이미지 스티칭은 동일 장면의 사진을 자연스럽게(seamless) 붙여서 한 장의 사진으로 만드는 기술입니다. 사진 이어 붙이기, 파노라마 영상(Panorama image) 기본적인 방법은 여러장의 영상에서 특징점을 검출하고 특징점이 동일한 것들을 찾아서 두 장의 영상과의 투시변환 관계를 찾아내어 이어 붙입니다. 위 두 영상에서 특징점을 검출 시 하늘에서는 특징점이 검출되지 않습니다. 엣지가 있고 지글지글한 텍스쳐가 있는 부분만 특징점이 검출됩니다. 위 그림에서 양쪽에 검출된 특징점만 남겨둡니다. 매칭되는 정보를 이용해서 투시변환 관계를 추출하고 이어 붙입니다. 단순히 이어 붙이면 밝기가 급격히 바뀌는 부자연스러움이 생깁니다. 밝기를 부드럽게 할 수있는 블렌딩..

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 회귀계수(기울기)에 대한 통계적 추론 회귀계수 중 기울기에 해당하는 $\beta_1$의 중심축량, 구간추정, 가설검정에 대해 알아보겠습니다. 1. 기울기 $\beta_1$에 대한 추론 $\hat{\beta_1}$은 $\beta_1$의 추정값입니다. $\hat{\beta_1} = S_{xY}/S_{xx}$의 통계적 성질은 다음과 같습니다. $\hat{\beta_1}$의 기댓값은 다음과 같이 구할 수 있습니다. $\hat{\beta_1}$의 분산은 다음과 같습니다. $\hat{\beta_1}$의 기댓값과 분산을 구했으므로 $\hat{\beta_1}$는 다음과 같이 가정할 수 있습니다. 이를 표준화하면 중심축량을 구할 수 있습니다...

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 회귀추론을 위한 기본이론 회귀모형의 모수 또는 예측값을 추론을 위한 기본 통계이론을 정리하겠습니다. 1. 회귀 모형식 가정 단순회귀모형에서 모형식은 다음과 같이 가정할 수 있습니다. 여기서, $\beta_0 + \beta_1x_i$는 평균을 의미합니다. $\epsilon_i$ ~ iid N(0,$\sigma^2$)는 추론할 때 필요한 가정입니다. 최소제곱법에 의한 모수 추정에서는 특별히 오차항의 가정을 사용하지 않습니다. 최소제곱법은 $y_i - \beta_0 - \beta_1x_i$를 이용하기 때문에 $\epsilon_i$는 신경쓰지 않는다는 의미입니다. 모수 추정량 또는 예측값의 성질을 유도하기 위해 오차항의 가정이 필요합..

호모그래피와 영상 매칭 호모그래피(Homography)는 두 평면 사이의 투시 변환(Perspective transform)을 의미합니다. 위 그림에서 v1 지점에서 바닥에 있는 사진을 카메라로 찰영한다고 가정하겠습니다. 찰영한 사진은 I1 입니다. 왼쪽 위에서 찰영을 했기 때문에 영상도 좀 기울어지고 비스듬해집니다. 원래 사진과 기울어진 사진과의 관계를 호모그래피 H1이라고 표현합니다. 마찬가지로 v2 지점에서 바닥 사진을 찰영한 사진은 I2입니다. I2와 바닥 사진 관계를 호모그래피 H2로 표현합니다. 또한 I1과 I2도 호모그래피 H12 관계가 생깁니다. 호모그래피는 투시변환과 거의 유사합니다. 투시변환 행렬로 표현할 수 있습니다. 투시변환 행렬에서 h33은 상수이므로 8개의 미지수로 구성됩니다. ..

이전 포스팅에서 특징점을 매칭하는 방법에 대해 공부해보았습니다. 하지만 결과값이 너무 복잡하여 매칭이 잘 되었는지 확인하는 것에 어려움이 있었습니다. 이번에는 좋은 매칭을 선별하는 두 가지 방법에 대해 공부해보겠습니다. [파이썬 OpenCV] 두 영상의 특징점 매칭과 매칭 결과 그리기 - cv2.BFMatcher_create, cv2.DescriptorMatcher, cv2. 두 영상에서 검출한 특징점을 서로 매칭하는 방법을 공부해보겠습니다. 특징점 매칭 - Feature point matching 특징점 매칭은 두 영상에서 추출한 특징점 기술자를 비교하여 서로 유사한 기술자를 � deep-learning-study.tistory.com 좋은 매칭 선별 좋은 매칭 선별 방법 두 가지를 알아보겠습니다. 1..

두 영상에서 검출한 특징점을 서로 매칭하는 방법을 공부해보겠습니다. 특징점 매칭 - Feature point matching 특징점 매칭은 두 영상에서 추출한 특징점 기술자를 비교하여 서로 유사한 기술자를 찾는 작업입니다. 왼쪽은 4개의 기술자, 오른쪽은 3개의 기술자를 계산했습니다. 가장 비슷한 것을 찾으므로 4개의 점은 다 매칭이 될 것입니다. 위 그림에서 #3이 잘못 매칭된 것을 확인할 수 있는데 알고리즘은 가장 거리가 짧은 곳을 찾아서 매칭을 하기 때문에 매칭이 되었습니다. 이처럼 잘못 연결된 매칭을 걸러내는 작업을 해야합니다. [특징 벡터 유사도 측정 방법] (1) 실수 특징 벡터 : L2 노름(L2 norm) 사용 (2) 이진 특징 벡터 : 해밍 거리(hamming distance) 사용 1...

특징점 기술 OpenCV로 영상의 특징점을 기술하는 방법을 공부하기 전에 기술자 or 특징벡터에 대하여 먼저 공부하겠습니다. 1. 기술자 - Descriptor, Feature vector 기술자는 특징벡터라는 용어로 같이 이용되고 있습니다. 기술자는 검출된 특징점 근방의 부분 영상을 표현하는 실수 또는 이진 벡터를 의미합니다. 실수값으로 표현한 영상의 모양 혹은 색상 분포로 이해하면 됩니다. OpenCV에서는 2차원 행렬(numpy.ndarray)로 표현합니다. 행 개수는 특징점 개수, 열 개수는 특징점 기술자 알고리즘에 의해 다르게 정의됩니다. KAZE 특징점 검출 방법으로 3159개의 특징점을 검출했습니다. 이런 경우에 행은 3159개 열은 64개입니다. float32 이므로 하나 당 4바이트이고 ..

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 단순선형회귀모형에서의 모수 추정 설명변수가 하나인 회귀모형에서 관측값과 회귀선과의 거리를 어떻게 표시하는지 알아보겠습니다. 최소제곱법을 이용한 회귀모수를 추정하는 방법을 알아보겠습니다. 1. 단순선형회귀모형 - Simple Linear Regression Model 단순선형회귀모형은 설명변수가 하나인 선형회귀모형을 의미합니다. 회귀모형 중에서 가장 간단한 형태입니다. $x_i$를 소문자로 쓴 이유는 상수로 가정하기 때문입니다. 또한 $Y_i$ ~ iidN(0,$\sigma^2$)를 가정합니다. $\epsilon$은 오차(error)를 의미하며 모형에서 설명이 안되는 부분입니다. 설명변수(x)는 조절 가능한 상수로 가정합니다. ..

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 저번 포스팅에서는 다변량 자료의 관계를 파악하는 방법인 산점도와 상관분석에 대해 공부해보았습니다. 이번에는 수치변수들 간 인과관계를 설명하기 위한 대표적인 통계모형인 회귀모형을 알아보겠습니다. 다변량 자료에서 주요 관심사 다변량 자료에서 주요 관심사는 변수들 간의 관계입니다. 1. 산점도와 상관분석으로 분석 가능한 관심사 (1) 변수들 간 관계가 있는가? (2) 있다면 어떤 관계가 있는가? (3) 관계가 어느 정도 되는가? 위 세 개의 관심사는 산점도와 상관분석을 통해 직선관계를 파악하여 분석할 수 있습니다. 산점도와 상관분석은 직선관계만 파악할 수 있습니다. 2. 회귀모형으로 분석 가능한 관심사 (1) 관계를 식으로 표시할 ..

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 수치변수들 간의 관계를 간단히 알아보는 방법을 알아보겠습니다. 회귀 분석을 공부하기 전에 다변량 자료가 무엇인지 복습을 해보도록 하겠습니다. 다변량 자료 - Multivariate Data 다변량 자료는 어떤 대상에 대해 여러 가지 변수들을 관측(측정)한 자료들의 집함을 의미합니다 예) 신체검사 자료에서 연령, 성별, 신장, 체중 시력, 혈액형 등등 자료의 형태를 보면 변수가 여러개 인것을 확인할 수 있습니다. 이를 다변량 자료라고 합니다. 변수가 하나면 일변량 자료 입니다. 각각의 관측값 간에는 관력성이 없습니다. 이는 독립적인 관측값을 의미합니다. 다음에 배울 회귀 분석에서는 독립적인 관측값을 가정합니다. 다변량 자료에서의..