여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
자료들의 변동을 요소별로 분해하여 정리한 분산분석표에 대해 알아보겠습니다.
고정효과모형과 변량효과모형에서 F통계량의 분모와 분자인 평균제곱의 통계적 성질을 알아보겠습니다.
변동분해
모형식을 정리하여 변동을 요소별로 분해할 수 있습니다.
모형식이 다음과 같을때, TSS(변동), SSE(잔차제곱합), SSTR(처리제곱합) 으로 분해할 수 있습니다.
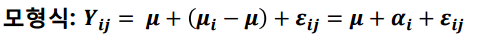
$\mu$는 평균, $\alpha$는 처리효과, $\epsilon$은 오차를 의미합니다.
모형식을 정리하면 다음과 같이 표현할 수 있습니다.
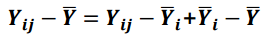
이 식을 제곱한 값을 모두 더해주면 다음과 같이 됩니다.
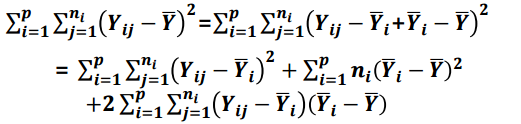
이 식을 정리하면 세 가지 변동으로 분해됩니다.
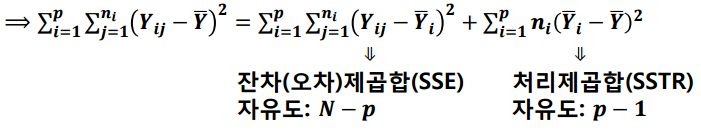
SSE + SSTR = TSS가 됩니다.
평균제곱(Mean Squares)
평균제곱은 SS를 자유도로 나눈 값입니다.
평균제곱오차(Mean Squares Error)
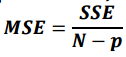
평균제곱처리(Mean sqaures due to treatment)
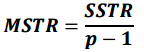
MSE와 MSTR을 이용하면 검정통계량을 나타낼 수 있습니다.
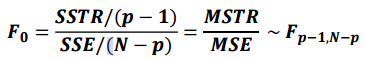
검정통계량은 F분포를 따르게 됩니다.
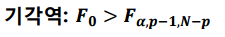
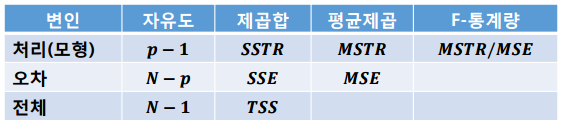
분산분석표(ANOVA Table)
모형의 요소들을 분해해서 분산분석표를 작성한다면 통계값을 쉽게 구할 수 있습니다.
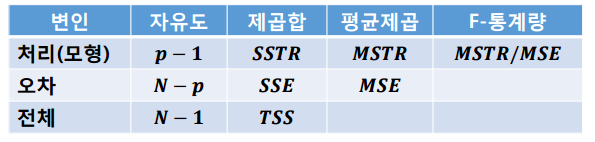
처리는 모형으로 설명가능한 값이고 오차는 모형으로 설명이 안되는 값입니다.
고정효과모형에서 평균제곱(MS)의 통계적 성질
고정효과모형은 요인이 하나이고 수준은 사용자가 임의대로 결정하는 모형입니다.
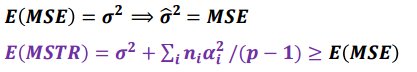
귀무가설이 참일 때만 등호가 성립하게 됩니다.
MSTR이 ME보다 크며 클수록 처리효과가 0이 아닐 가능성이 높아집니다.
분산분석결과 귀무가설을 기각시키지 못한 경우에는 처리 간에 차이가 없으므로 추가분석이 필요하지 않습니다.
분산분석결과 귀무가설을 기각시키는 경우 어떤 처리 간에 차이가 있는지 또는 어떤 그룹들 간에 차이가 있는지 등을 알아볼 수 있습니다.
변량효과모형에서의 평균제곱(MS)의 통계적 성질
변량효과모형은 요인이 하나이고 수준은 무작위로 선택하는 경우를 의미합니다.
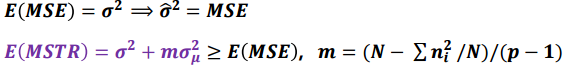
변량효과모형에서 평균값은 확률변수로 취급하므로 분산에 관심을 갖습니다.
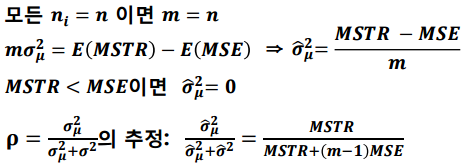
추정하여 $\rho$값으로 상관관계를 구할 수 있습니다.
정리
(1) 분산분석표
자료들의 변동을 요소별로 분해하여 정리한 분산분석표
(2) 고정효과모형과 변량효과모형에서 F통계량의 분모와 분자인 평균제곱의 통계적 성질
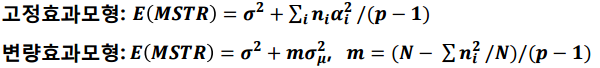
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 분산분석 - 다중비교 - Fisher LSD, Bonferroni, Scheffe, Tukey HSD (0) | 2020.10.10 |
|---|---|
| [통계학] 분산분석 - 등분산성 검정 - 잔차그림, Hartley 검정, Bartlett 검정 (0) | 2020.10.10 |
| [통계학] 분산분석 - 변량효과모형 - 요인이 하나, 수준을 무작위 (0) | 2020.10.08 |
| [통계학] 일원배치 분산분석 - 고정효과모형 - 요인이 하나 수준은 임의적 (0) | 2020.10.08 |
| [통계학] 분산분석에서의 용어와 개념 - 실험계획법, 설명변수, 공변량, 요인, 반응변수, 처리, 수준 (0) | 2020.10.07 |