(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다.
다양한 확률 및 통계문제를 해결하기 위해 기댓값의 성질에 대해 알아보도록 하겠습니다.
1. 기댓값 - expected value
기댓값은 확률변수에 대해 평균적으로 기대하는 값이라는 의미를 갖은 용어로 평균과 같은 개념입니다. 그래서 $X$의 평균을 $X$의 기댓값이라고 하고 $E(X)$로 표시합니다. 즉 $E(X) = \mu $가 됩니다.
기댓값을 설명하기 위해 모평균을 설명하도록 하겠습니다.
모평균은 표본평균에서 표본크기 n을 계속 크게하여 통계적 확률의 관점에서 볼 때 표본들은 모집단으로, 표본평균은 모평균으로 수렴한 것을 의미합니다.
모평균을 설명하기 위해 표본평균을 설명하도록 하겠습니다.
이산모집단으로부터 임의로 5개의 표본을 선택하였는데 그 값이 각각 1, 1, 2, 5, 6이라고 하겠습니다. 이 표본들의 표본평균을 $\overline{x}$라고 하면 다음과 같은 식이 도출됩니다.

위의 식에서 보면 표본평균은 관측된 값에 그 값이 차지하는 표본비율을 곱하여 더한 것으로 표시됩니다. 만약 표본크기가 $n$이고 자료 중 서로 다른 값이 $k$개가 있어 이들 값을 $x_1, ... , x_k$라고 하겠습니다. 표본 중 $x_i$의 값을 가지는 자료의 개수를 $n_i$라고 하면 다음과 같이 도출할 수 있습니다.

여기서 $p_i = n_i/n$은 $n$개 중에서 $x_i$의 값을 가지는 표본의 비율입니다.
이를 정리하면 표본평균은 관측 자료의 값에 해당 자료의 비율을 곱하여 다 더한 값이 됩니다.
표본크기 $n$을 계속 크게 하면 통계적 확률의 관점에서 볼 때 표본들은 모집단으로, 표본비율 $p_i$는 확률질량함수 $f(x_i)$로, 표본평균은 모평균으로 수렴할 것 입니다. 즉, n이 계속 커지면 다음과 같이 됩니다.

통계학에서는 확률변수 $X$의 모평균(population mean)을 $\mu$로 표기하며 다음과 같이 정의합니다. 표본평균이 자료들의 무게중심이듯이 평균은 확률분포(또는 모집단)의 무게중심이 됩니다. 기댓값은 확률변수에 대해 평균적으로 기대하는 값이라는 의미이므로 평균과 같은 개념입니다. 따라서 다음 같은 식이 도출될 수 있습니다.
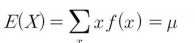
연속확률변수의 기댓값은 확률밀도함수에 단위길이 $dx$를 곱하여 다음과 같이 표시할 수 있습니다.

확률변수 $X$ 대신 $W = (X )^2$의 기댓값에 관심을 갖는다고 해보겠습니다.

W = 1일때는 x가 -1, 1인 두가지 경우이므로 두 확률을 더해서 구해줍니다.
W의 기댓값은 다음과 같이 구할 수 있습니다.

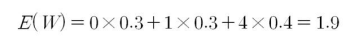
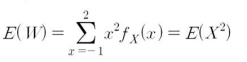
이를 일반식으로 정리하면 다음과 같습니다.
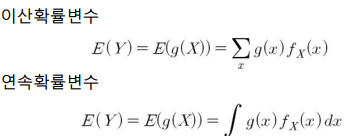
이번에는 확률변수 $X$의 선형식, $aX + b$에 관심을 갖는다고 해보겠습니다. 확률변수의 선형식에 대한 기댓값은 다음과 같이 기댓값의 선형식으로 표시할 수 있습니다.

또한 확률변수 $X$의 여러 식에 대한 더하기나 빼기의 기댓값은 다음과 같이 이들 식의 기댓값을 더하거나 뺀 값으로 표시할 수 있습니다.

이상으로 기댓값의 성질에 대해서 알아보았습니다. 감사합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 08-2. 확률벡터(2) - 결합분포, 주변분포, 독립확률변수 (0) | 2020.09.18 |
|---|---|
| [통계학] 08-1. 확률벡터(1) - 분산과 표준편차 (0) | 2020.09.18 |
| [통계학] 07-4. 연속확률변수와 확률밀도함수 (0) | 2020.09.17 |
| [통계학] 07-3. 이산확률변수와 확률질량함수 (확률질량함수의 성질, 확률함수의 변환, 누적분포함수) (0) | 2020.09.17 |
| [통계학] 07-2. 확률분포, 확률분포표 (0) | 2020.09.17 |