(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다.
두 확률변수의 확률구조를 설명하기 위한 결합분포와 주변분포에 대해 알아보겠습니다.
결합분포와 주변분포의 관계로부터 두 확률분포가 독립인지 아닌지를 확인하는 방법을 알아보겠습니다.
1. 확률벡터 - random vector
확률벡터: 확률변수를 순서열 $(X_1, X_2, ... ,X_p)$로 표시한 것을 확률벡터라고 합니다.
설명
자료를 수집할 때 특정 변수 하나만 관심을 가질 수 있으나 여러 가지 변수의 자료를 얻고 이들 변수들 간에 어떤 관계가 있는지 관심을 가질 수도 있습니다. 아이돌 가수 프로필 자료에서 신장, 체중 등의 여러 변수에 대한 자료를 수집하고 이에 대한 관계분석을 할 수 있습니다. 이렇게 여러 가지 확률변수를 순서열 $(X_1, X_2, ... , X_p)$로 표시한 것을 확률벡터라고 합니다.
동전을 3번 던진 실험에서 앞면의 수 $X$와 앞면과 뒷면의 차이 $Y$를 표본공간과 연결하여 다음과 같은 결과를 얻을 수 있습니다.

$X$와 $Y$는 각각 표본공간상에서 정의된 확률변수이며 이들 확률변수로 이루어진 벡터 $(X, Y)$는 확률벡터가 됩니다.
2. 결합분포 - joint distribution
결합분포는 두 개 이상의 확률변수들을 동시에 고려한 확률분포 입니다.
두 이산확률변수 $X$와 $Y$에 대해 다음과 같이 표시할 수 있습니다.

n개의 이산확률변수 $X_1, ... ,X_n$에 대해 다음과 같이 표시할 수 있습니다.
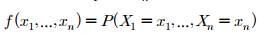
이변량 분포(bivariate distribution) : 두 확률변수의 결합분포
다변량 분포(p - dimensional multivariate distribution) : p 개의 확률변수로 이루어진 확률벡터의 결합분포
설명
(1) 이산확률변수의 경우 결합확률질량함수
두 이산확률변수 $X$와 $Y$에 대해, $X = x$이고 $Y = y$일 확률은 다음과 같은 함수 $f(x,y)$로 정의하면 다음과 같습니다.

여기서 $f(x,y)$를 확률변수 $X$와 $Y$의 결합확률질량함수(joint probability mass function)이라고 합니다. 위 식에서 ,는 집합에서 $\cap$을 의미합니다.
그러므로 모든 $x, y$에 대해 $0 \leq f(x,y) \leq 1$이고 $\sum_a\sum_af(x,y) = 1$가 성립하게 됩니다.
동전 세번 던지기 예시를 표로 정리하면 다음과 같습니다.

이를 결합확률질량함수로 표시하면
$$f(0,3) = \frac{1}{8}, f(1,1) = \frac{3}{8}, f(3,3) = \frac{1}{8}$$
이 됩니다.
(2) 연속확률변수의 경우 결합확률밀도 함수
연속확률변수의 경우 결합확률밀도함수 $f(x,y)$는 $(x,y)$에서 밀도가 상대적으로 얼마나 높은지를 나타내는 것으로 다음과 같은 특징이 있습니다.

3. 주변분포 - marginal distribution
주변분포는 두 이산확률변수 $X$와 $Y$의 결합확률질량함수가 $f(x,y)$일 때, $X$의 확률질량함수는 모든 $y$의 결합확률질량함수를 더하여 구할 수 있는 것을 의미합니다.


이 표에서 주변에 있는 확률의 합은 각 확률변수가 가질 수 있는 값에 대한 확률로 $Y$의 주변확률질량함수는 다음과 같습니다.
$$f_y(1) = f(0,1) + f(1,1) + f(2,1) + f(3,1) = \frac{3}{4}$$
설명
(1) 이산확률변수일 경우 주변확률질량함수
주변분포를 설명하기 위해 조건부확률에서 공부하였던 분할이 필요합니다.
표본공간이 사건 $B_1, ... ,B_n$로 분할될 때 사건 $A$의 확률은 다음과 같습니다.
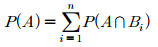
만약 $Y$가 가질 수 있는 값이 $y_1, ... ,y_n$이라고 할 때, $X = x$를 사건 $A$, $Y = y_i$를 사건 $B_i$라고 하면 다음의 식을 생각할 수 있습니다.

이 식을 이용하면 $P(A)$는 다음의 관계가 성립하게 됩니다.
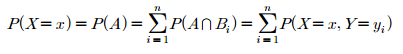
이것은 두 이산확률변수 $X$와 $Y$의 결합확률질량함수 $f(x, y)$일 때, $X$의 확률질량함수는 다음과 같이 모든 $y$의 결합확률질량함수를 더해 구할 수 있다는 것을 의미합니다.

이 경우 $f_X(x)$를 $X$의 주변확률질량함수(marginal density function)라고 하며 $Y$의 주변확률질량함수도 다음과 같이 유도합니다.
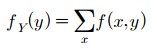
(2) 연속확률변수일 경우 주변확률밀도함수
확률질량함수와 마찬가지로 주변확률밀도함수는 다음과 같이 다른 확률변수에 대해 적분하여 구할 수 있습니다.
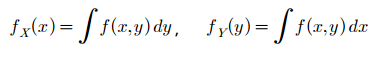
3. 독립 확률변수
두 확률변수가 독립이라면 한 확률변수가 어떤 값을 갖더라도 다른 변수의 확률에 영향을 주지 않는다는 것을 의미합니다. 조건부확률에서 공부하였던 독립 사건을 이용하여 결합확률질량(밀도)함수가 주변확률질량(밀도)함수의 곱으로 표기할 수 있습니다.
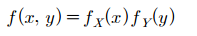
이는 확률변수 $X$와 $Y$는 독립(independent)라고 합니다.
세 개 이상의 확률변수의 독립성도 같은 개념으로 정의할 수 있습니다.

설명
독립 확률변수는 독립사건을 이용한 것입니다. 두 사건 A와 B의 독립성에 대한 필요충분조건은 다음과 같습니다.
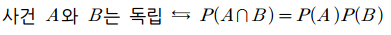
여기에서는 사건이 아닌 두 확률변수의 독립에대해 알아보겠습니다. 두 확률변수가 독립이라면 한 확률변수가 어떤 값을 갖더라도 다른 변수의 확률에 영향을 주지 않는다는 것을 의미합니다.
이를 위와 같은 방법으로 표시하면 두 확률변수 $X$와 $Y$가 모든 x,y에 대하여 결합확률질량(밀도)함수가 주변확률질량(밀도)함수의 곱으로 표시할 수 있습니다.

이런 경우 확률변수 $X$와 $Y$는 독립이라고 합니다.
두 확률변수 $X$와 $Y$가 독립이면 두 결합확률함수가 각각 주변확률함수의 곱으로 표시되고 확률변수가 가질 수 있는 값들이 서로 영향을 주지 않습니다.
그러므로 결합확률함수 $f(x,y)가 $x$만으로 이루어진 임의의 함수 $f_1(x)$와 $y$만으로 이루어진 함수 $f_2(y)$의 곱으로 표시되고 $x$의 구간과 $y$가 서로 영향을 주지 않으면 두 확률변수 $X$와 $Y$가 독립이라고 할 수 있습니다.
예시문제
$f(x,y) = x + y, 0 < x < 1, 0 < y < 1
위 식일때 $X$와 $Y$는 독립이 아닙니다. 왜냐라면 $f(x,y)$는 $x$와 $y$의 더하기 꼴로 $x$만의 함수와 $y$만의 함수의 곱으로 표시할 수 없기 때문입니다.
이상으로 두 확률변수의 확률구조를 설명하기 위한 결합분포와 주변분포에 대해 알아보았습니다.
결합분포와 주변분포의 관계로부터 두 확률분포가 독립인지 아닌지를 확인하는 방법을 알아보았습니다. 감사합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 09-1. 베르누이 시행, 베르누이 확률변수, 베르누이 분포 (0) | 2020.09.19 |
|---|---|
| [통계학] 08-3. 확률벡터(3) - 기댓값, 공분산, 상관계수 (1) | 2020.09.19 |
| [통계학] 08-1. 확률벡터(1) - 분산과 표준편차 (0) | 2020.09.18 |
| [통계학] 07-5. 확률변수의 기댓값 - 기댓값의 성질 (0) | 2020.09.18 |
| [통계학] 07-4. 연속확률변수와 확률밀도함수 (0) | 2020.09.17 |