(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다.
두 개 이상의 확률변수에 대한 기댓값 계산 방법을 알아보겠습니다.
두 변수의 직선관계 정도를 나타내는 공분산과 상관계수를 계산하고 독립일 때 이들 값이 0인 것을 보입니다.
두 변수의 선형결합과 관련된 평균과 분산의 성질에 대해 알아보겠습니다.
1. 기댓값 - expected value
두 확률변수 $X$와 $Y$에 대해 $X + Y$나 $XY$의 기댓값은 어떻게 계산해야 할까?
기댓값은 확률변수가 가질 수 있는 값에 해당 확률을 곱하여 다 더한 것으로 정의 했습니다.
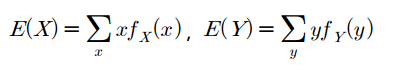
두 확률변수의 기댓값은 이들 변수가 가질 수 있는 값에 해당 확률, 즉 결합확률질량함수를 곱하여 $x$와 $y$에 대해 다 더한 것으로 표시합니다.
두 변수를 고려한다는 것은 두 변수에 대한 결합분포가 있다는 것을 전제합니다. 따라서 결합확률질량함수나 결합확률밀도함수를 이용해야 합니다.
확률변수 $X$와 $Y$가 이산확률변수이고 결합확률질량함수가 $f(x,y)$라고 하면, $X + Y$와 $XY$의 기댓값은 다음과 같이 됩니다.


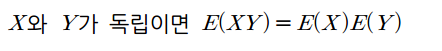
2. 공분산 - covariance
공분산은 두 확률변수의 직선관계 정도를 나타내는 측도입니다.
이전의 포스팅에서 표본공분산은 다음과 같이 정의했습니다.
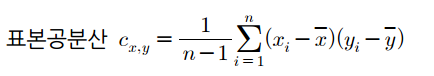
$X$와 $Y$의 공분산을 $Cov(X,Y)$라고 하면 두 확률변수 $X$와 $Y$의 공분산은 다음과 같이 됩니다.

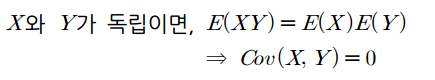
두 확률변수 $X$와 $Y$가 독립이면 $E(XY) = E(X)E(Y)$ 라는 것을 배웠습니다.
이것은 $X$와 $Y$가 독립이면 공분산 $Cov(X,Y) = 0$이 되는 것을 의미합니다.
하지면 $Cov(X,Y) = 0$이라고 $X$와 $Y$가 독립이지는 않습니다.

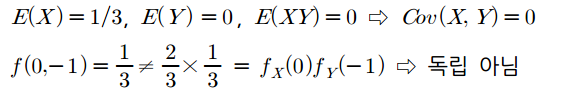
3. 상관계수 - coefficient of correlation
표본상관계수의 의미는 표준화변수들의 공분산을 의미합니다. 공분산에 표준편차를 나눠준 값입니다.
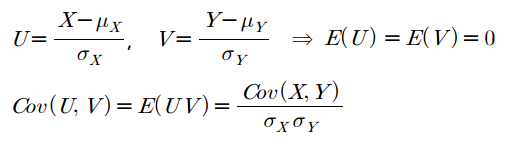
두 확률변수 $X$와 $Y$의 상관계수는 다음과 같이 표현할 수 있습니다.

$X$와 $Y$의 상관계수의 성질은 다음과 같습니다.

여기서 $sign(a)$는 a의 부호함수로 a가 양수이면 1, 음수이면 -1, 0이면 0의 값을 갖는 함수입니다.
4. 기댓값 정리

'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 09-2. 이항분포 (1) | 2020.09.19 |
|---|---|
| [통계학] 09-1. 베르누이 시행, 베르누이 확률변수, 베르누이 분포 (0) | 2020.09.19 |
| [통계학] 08-2. 확률벡터(2) - 결합분포, 주변분포, 독립확률변수 (0) | 2020.09.18 |
| [통계학] 08-1. 확률벡터(1) - 분산과 표준편차 (0) | 2020.09.18 |
| [통계학] 07-5. 확률변수의 기댓값 - 기댓값의 성질 (0) | 2020.09.18 |