실함수의 기하학(The Geometry of Real-Valued Functions)
실함수를 graph, level curve, level surface로 시각화하여 이해해보도록 하겠습니다.
함수와 사상(Fuctions and Mappings)
함수는 정의역(domain)으로 R^n 공간에 있는 부분 집합 A을 갖고 있고, 이 부분 집합을 R^m 공간에 있는 공역(codomain)으로 전달합니다.
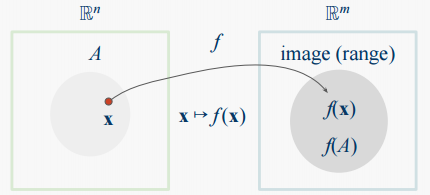
공역(codomain)의 차원에 따라 함수의 명칭이 달라집니다.
m > 1 인 경우 함수 f를 벡터 함수(vector-valued function)이라고 부릅니다.
m = 1 인 경우 함수 f를 스칼라 함수(scalar-valued function)이라고 합니다.
예를 들어, scalar-valued function은 정의역에 존재하는 x,y,z를 스칼라 값 f(x,y,z)로 전달합니다.

만약, 정의역(domain)의 차원 n이 1보다 크다면 다변수 함수(functions of several variables)라고 합니다.


그러면 위 함수는 어떤 함수일까요? 우선 정의역에 6개의 변수가 존재하고, g(x)가 두 개의 값으로 전달되므로 벡터 함수(vector valued function) 입니다. R^n에 존재하는 요소를 R^m으로 전달합니다.
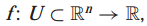
위 함수는 n개의 변수를 입력받아 1차원의 스칼라를 반환합니다. 이 함수를 정의역 U에서 n 변수를 가지는 실함수(real-valued function of n variables with domain)이라고 부릅니다.
함수의 그래프(Graphs of Functions)

그래프(graph)는 정의역에 존재하는 n개의 변수와 f(x_n)의 출력값의 모든 점들의 집합입니다.

그림(a)는 하나의 변수를 입력받는 함수이고, 그림(b)는 두개의 변수에 대한 함수입니다.
레벨 집합, 등위선, 등위면(Level Sets, Curves, Surfaces)
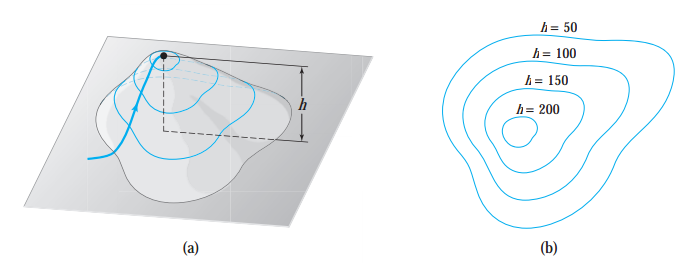
4차원 이상을 갖고 있는 함수의 그래프는 시각화하기가 불가능합니다. 현실 세계는 3차원 세상이기 때문입니다. 레벨 집합과 등위선, 등위면은 4차원 이상인 함수의 그래프를 시각화 하는데 도움을 줍니다. 위 그림은 3차원을 갖고 있는 그래프의 레벨 집합입니다. f(x,y)가 상수로 고정되어 graph = (x,y,f(x,y))을 2차원으로 표현할 수 있습니다.
level set은 f(x,y,z) = c(상수)를 만족하는 모든 x,y,z 집합입니다. 만약 함수가 이변수 함수 f(x,y)이면, 등위선(level curves) 또는 등고선(level contours)이라고 합니다.

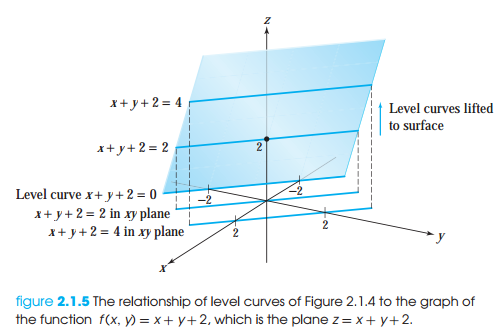
Level Curves와 Level Surfaces는 다음과 같이 정의합니다.

2개의 변수를 취하는 함수의 level set은 등위선(level curve)라고 부릅니다. f(x,y)=c를 만족하는 모든 x,y 집합이 선으로 표현되기 때문입니다.
3개의 변수를 취하는 함수의 level set은 등위면(level surface)라고 부릅니다. f(x,y,z)=c를 만족하는 모든 x,y,z 집합이 3차원 공간에서 면으로 표현되기 때문입니다.


단면 활용법(The Method of Sections)
단면(Section)은 함수의 그래프와 평면과의 교집합을 의미합니다. 만약, 함수 f가 다음과 같이 정의되고, 단면이 y=0으로 정의되는 xz 평면이라면 f의 단면은 다음과 같이 정의합니다.

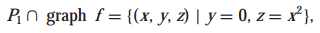
x=0으로 정의되는 xz평면과의 함수의 그래프의 단면은 다음과 같습니다.


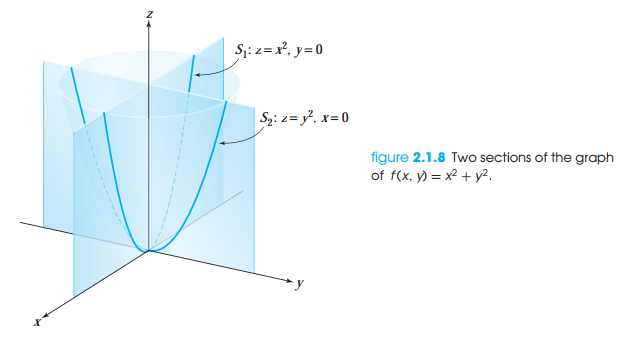
참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus
'수학 > 벡터 미적분학' 카테고리의 다른 글
| [벡터 미적분학] 극한(Limits)과 극한의 성질(Properties of Limits) (0) | 2021.06.02 |
|---|---|
| [벡터 미적분학] 경계점(Boundary Points) (0) | 2021.06.01 |
| [벡터 미적분학] 평면의 방정식(Equations of Planes) (0) | 2021.05.31 |
| [벡터 미적분학] 열린 집합(Open Sets), 열린 원판(Open Disk), x의 근방(Neighborhood of x) (0) | 2021.05.31 |
| [백터 미적분학] 직선의 방정식(Equations of Lines) (0) | 2021.05.30 |