반응형
열린 집합과 열린 원판(Open Set and Open Disk)
열린 집합은 극한의 개념을 이해하기 위해서 필요합니다. 열린 집합(open set)을 알아보기 전에 열린 원판(open dist)을 정의하겠습니다.
(1) 열린 원판(Open Dist)
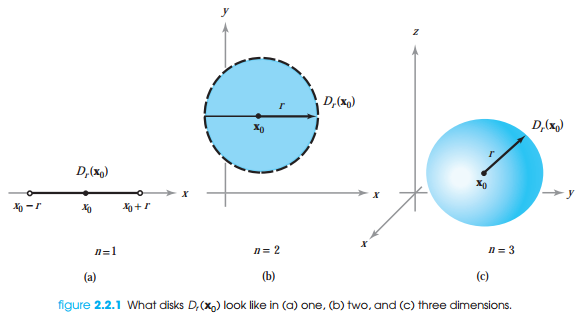
열린 원판은 양의 실수 r과 x_0에 대하여 llx-x_0ll < r을 만족하는 모든 점 x의 집합을 의미합니다. 열린 원판은 원의 중심이 x_0이고, 반지름이 r인 원의 안쪽에 존재하는 모든 점 x를 의미합니다. 정리하면, x_0으로부터 거리가 r보다 작은 모든 점 x를 의미합니다. 그리고 Dr(x_0)으로 표기합니다.
(2) 열린 집합(Open Set)


열린 집합은 열린 원판 Dr(x_0)이 U에 존재하고, U가 R^n의 부분집합인 경우에 이 U를 열린 집합이라고 합니다. 정의에 의해 공집합도 열린 집합이 됩니다. 또한 열린 원판도 열린 집합입니다.

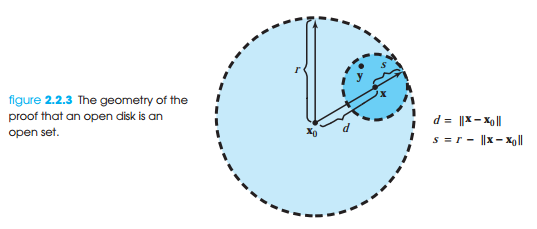
위 그림처럼 열린 원판내에 또다른 열린 원판이 존재하므로 열린 원판은 열린 집합이라고 볼 수 있습니다.
(3) x의 근방(Neighborhood of x)
주어진 점 x를 포함하는 열린 집합을 x의 근방이라고 합니다. 즉, 점 x를 포함하는 열린 집합 U를 단순히 x의 근방(neighborhood of x)이라고 합니다.
참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus
반응형
'수학 > 벡터 미적분학' 카테고리의 다른 글
| [벡터 미적분학] 극한(Limits)과 극한의 성질(Properties of Limits) (0) | 2021.06.02 |
|---|---|
| [벡터 미적분학] 경계점(Boundary Points) (0) | 2021.06.01 |
| [벡터 미적분학] 평면의 방정식(Equations of Planes) (0) | 2021.05.31 |
| [백터 미적분학] 직선의 방정식(Equations of Lines) (0) | 2021.05.30 |
| [벡터 미적분학] 그래프(Graph), 레벨 집합(Level set), 단면(Section) (1) | 2021.05.29 |