반응형
직선의 방정식(Equations of Lines)
평면과 직선은 방정식으로 표현될 수 있는 기하학적인 객체입니다. 여기서는 직선의 방정식을 벡터 덧셈, 스칼라 곱을 사용하여 알아보겠습니다. 벡터 a의 끝점을 통과하고 벡터 v의 방향인 직선의 방정식은 다음과 같이 표현합니다.

t는 모든 실수이고, tv는 벡터 v의 모든 스칼라 곱입니다. 직선 l은 a와 tv를 변으로하는 평행사변형의 모든 대각 요소의 끝접이며, l = a + tv로 표현합니다. 즉, a의 끝점을 지나고 방향이 v인 직선의 방정식은 l = a + tv 입니다.

예제 문제를 한번 살펴보겠습니다.



동일한 직선은 여러가지 방정식으로 나타낼 수 있습니다. 주어진 선에서 a 대신에 다른 점을 선택하면 됩니다. 예를 들어, 직선의 방정식 l = a + tv 가 존재하는 경우에 l = (a+v) + tv는 동일한 직선을 나타냅니다. (a+v)가 직선 l에 존재하는 점이기 때문입니다.
두 벡터 a,b의 끝점을 지나는 직선의 방정식은 다음과 같이 구할 수 있습니다.
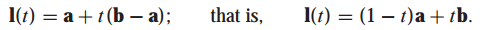

(b-a)가 직선의 방향을 나타내므로 l = a + t(b-a)로 표현할 수 있습니다.
공간에서 두 점이 주어졌고, 두 점을 지나는 직선의 방정식은 다음가 같이 구합니다.
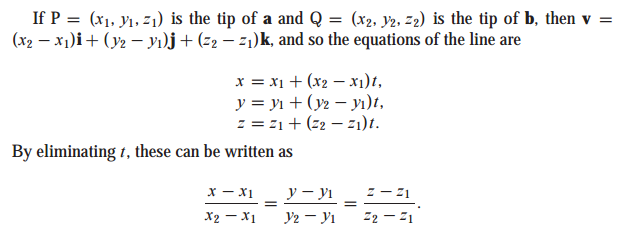
참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus
반응형
'수학 > 벡터 미적분학' 카테고리의 다른 글
| [벡터 미적분학] 극한(Limits)과 극한의 성질(Properties of Limits) (0) | 2021.06.02 |
|---|---|
| [벡터 미적분학] 경계점(Boundary Points) (0) | 2021.06.01 |
| [벡터 미적분학] 평면의 방정식(Equations of Planes) (0) | 2021.05.31 |
| [벡터 미적분학] 열린 집합(Open Sets), 열린 원판(Open Disk), x의 근방(Neighborhood of x) (0) | 2021.05.31 |
| [벡터 미적분학] 그래프(Graph), 레벨 집합(Level set), 단면(Section) (1) | 2021.05.29 |