반응형
평면의 방정식(Equations of Planes)
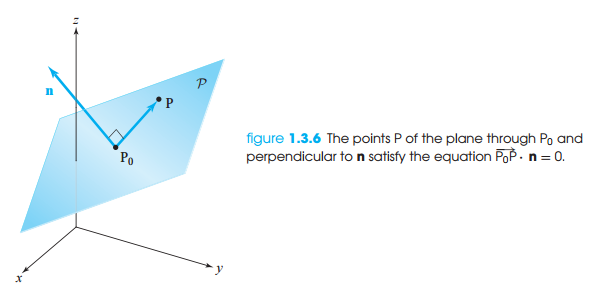
공간 내에 평면이 존재하고, 평면 위에 한 점 P0 = (x0, y0, z0)이 존재한다고 가정하겠습니다. 평면과 직교하는 법선 벡터(normal vector) n = Ai + Bj + Ck가 주어진 경우에 평면의 방정식은 어떻게 구해야 할까요? 우선 평면 위의 두점 P = (x,y,z)와 P0를 잇는 벡터와 법선 벡터 n은 직교합니다. 두 벡터가 직교하면 내적이 0이므로 이 성질을 이용하여 평면의 방정식을 계산할 수 있습니다.

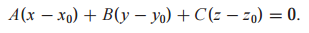

A, B, C, D는 유일하지 않습니다. 법선 벡터가 평행한 경우에도 해당 법선 벡터는 평면과 직교하기 때문입니다.
점에서 평면에 이르는 거리(Distance from a Point to a Plane)

공간에서 한 점 E와 평면 사이의 거리는 어떻게 구할까요?
우선 평면에 대한 unit normal vector을 구합니다. normal vector는 평면상의 두 벡터사이에 외적을 적용하여 구할 수 있습니다. 여기에 normalize를 적용하면 unit normal vector가 됩니다.

평면 위의 한 점 R = (x0, y0, z0)과 E = (x1, y1, z1) 사이를 잇는 벡터 v를 unit normal vector에 사영(projection)한 뒤에 계수 값만 가져오면 거리를 구할 수 있습니다.


참고자료 및 그림 출처
Jerrold E. Marsden의 Vector Calculus
반응형
'수학 > 벡터 미적분학' 카테고리의 다른 글
| [벡터 미적분학] 극한(Limits)과 극한의 성질(Properties of Limits) (0) | 2021.06.02 |
|---|---|
| [벡터 미적분학] 경계점(Boundary Points) (0) | 2021.06.01 |
| [벡터 미적분학] 열린 집합(Open Sets), 열린 원판(Open Disk), x의 근방(Neighborhood of x) (0) | 2021.05.31 |
| [백터 미적분학] 직선의 방정식(Equations of Lines) (0) | 2021.05.30 |
| [벡터 미적분학] 그래프(Graph), 레벨 집합(Level set), 단면(Section) (1) | 2021.05.29 |