딥러닝 공부방

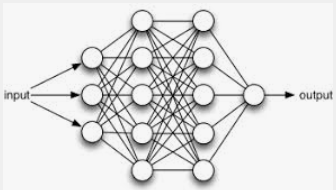
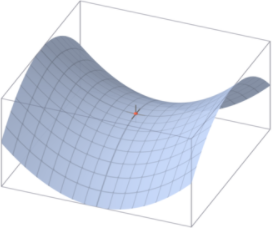
사이토고키의 을 공부하고 정리하였습니다. AdaGrad 신경망 학습에서는 학습률 값이 중요합니다. 이 값이 너무 작으면 학습 시간이 너무 길어지고, 반대로 너무 크면 발산하여 학습이 제대로 이뤄지지 않습니다. 이 학습률을 정하는 효과적 기술로 학습률 감소(learning rate decay)가 있습니다. 이는 학습을 진행하면서 학습률을 점차 줄여가는 방법입니다. 학습률을 서서히 낮추는 가장 간단한 방법은 매개변수 '전체'의 학습률 값을 일괄적으로 낮추는 것입니다. 이를 더욱 발전시킨 것이 AdaGrad입니다. AdaGrad는 '각각의' 매개변수에 '맞춤형'값을 만들어 줍니다. AdaGrad는 개별 매개변수에 적응적으로 학습률을 조정하면서 학습을 진행합니다. AdaGrad의 갱신 방법은 수식으로는 다음과 ..

사이토고키의 을 공부하고 정리해보았습니다. 모멘텀 - Momentum 모멘텀은 '운동량'을 뜻하는 단어로, 물리와 관계가 있습니다. 모멘텀 기법은 수식으로 다음과 같이 쓸 수 있습니다. SGD와 비교해보았을 때 v라는 변수가 새로 나옵니다. 이는 물리에서 말하는 속도에 해당합니다. 기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙을 나타냅니다. 모멘텀 구현 코드 class Momentum: def __init__(self, lr=0.01, momentum=0.9): self.lr = lr self.momentum = momentum self.v = None def update(self, params, grads): if self.v is None: self.v = {} for key, val in ..

사이토고키의 을 공부하고 정리하였습니다. 신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것 입니다. 이는 곧 매개변수의 최적값을 찾는 문제이며, 이를 최적화(optimization)이라고 합니다. 1. 확률적 경사 하강법(SGD) 매개변수의 기울기를 구해, 기울어진 방향으로 매개변수 값을 갱신하는 일을 몇 번이고 반복해서 점점 최적의 값에 다가가는 것이 확률적 경사 하강법(SGD)입니다. SGD는 수식으로 다음과 같이 쓸 수 있습니다. 여기에서 W는 갱신할 가중치 매개변수고 $\frac{\partial L}{\partial W}$은 W에 대한 손실 함수의 기울기 입니다. $\eta$는 학습률을 의미하는데, 0.01이나 0.001과 같은 값을 미리 정해서 사용합니다. SGD는 기..

(밑바닥부터 시작하는 딥러닝, 사이토고키)를 바탕으로 제작하였습니다. 오차역전파법(4) - 오차역전파법을 사용한 학습 구현 이전의 포스팅에서는 역전파를 적용한 활성화함수(ReLu, Sigmoid) 계층, Affine 계층, Softmax-with-Loss 계층을 구현해 보았습니다. 이번 포스팅에서는 지금까지 구현한 계층을 조합해서 오차역전파법을 사용한 학습을 구현해보겠습니다. 7. 오차역전파법 구현하기 7.1 신경망 학습의 전체 그림 우선 신경망 학습의 전체 그림을 복습해보겠습니다. 다음은 신경망 학습의 순서입니다. 전체 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 합니다. 신경망 학습은 다음과 같이 4단계로 수행합니다. 1단계 ..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 제작하였습니다. 오차역전파법 (3) - 활성화 함수, Affine, Softmax 계층 구현 이전의 포스팅에서는 사과 쇼핑 문제를 통해 간단한 역전파 계층을 구현해 보았습니다. 이번 포스팅에서는 활성화 함수(ReLu, Sigmoid) 계층, 행렬의 곱을 의미하는 Affine 계층, 출력층에서 사용하는 소프트맥스 계층을 구현해보도록 하겠습니다. 5. 활성화 함수 계층 구현하기 이제 계산 그래프를 신경망에 적용해보겠습니다. 우선 활성화 함수인 ReLu와 Sigmoid 계층을 구현하겠습니다. 5.1 ReLU 계층 활성화 함수로 사용되는 ReLU의 수식은 다음과 같습니다. x에 대한 y의 미분은 다음처럼 구합니다. 순전파 때의 입력인 x가 0보다 크면 역전..

(밑바닥부터 시작하는 딥러닝, 사이토고키)를 바탕으로 작성하였습니다. 오차역전파법 (2) - 간단한 역전파의 계층 구현 이전 포스팅에서는 역전파의 이해를 돕기 위해 계산 그래프의 역전파가 연쇄법칙에 따라 진행되는 모습을 공부하였습니다. 이번 포스팅에서는 사과 쇼핑의 예를 통해 간단한 역전파의 계층을 구현해보겠습니다. 3. 역전파 '+'와 'X' 등의 연산을 예로 들어 역전파의 구조를 설명하겠습니다. 3.1 덧셈 노드의 역전파 먼저 덧셈 노드의 역전파입니다. 여기에서는 $z = x + y$라는 식을 대상으로 역전파를 살펴보겠습니다. 우선, $z = x + y$의 미분은 다음과 같이 해석적으로 계산할 수 있습니다. $$\frac{\partial z}{\partial x} = 1$$ $$\frac{\parti..

(밑바닥부터 시작하는 딥러닝, 사이토고치) 를 바탕으로 작성하였습니다. 오차역전파법 (1) - 계산 그래프와 연쇄법칙 이전의 포스팅에서는 신경망 학습을 공부했습니다. 그때 신경망의 가중치 매개변수에 대한 손실 함수의 기울기는 수치 미분을 사용해 구했습니다. 수치 미분은 단순하고 구현하기도 쉽지만 계산 시간이 오래 걸린다는 게 단점입니다. 이번 포스팅에서는 가중치 매개변수의 기울기를 효율적으로 계산하는 '오차역전파법(backpropagation)'을 이해하기 위해 계산 그래프와 연쇄법칙에 대해 공부하겠습니다. 1. 계산 그래프 - Computational graph 계산 그래프(computational graph)는 계산 과정을 그래프로 나타낸 것입니다. 여기에서 그래프는 복수의 노드(node)와 에지(e..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다. 신경망 학습 (3) - 학습 알고리즘 구현 지금까지 배운 내용을 이용해서 신경망 학습 알고리즘을 구현해보겠습니다. 5. 학습 알고리즘 구현하기 신경망 학습의 절차는 다음과 같습니다. 전체 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 합니다. 신경망 학습은 다음과 같이 4단계로 수행합니다. 1단계 - 미니배치 훈련 데이터 중 일부를 무작위로 가져옵니다. 이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실 함수 값을 줄이는 것이 목표입니다. 2단계 - 기울기 산출 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구합니다. 기울기는 손..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다. 신경망 학습 (2) - 기울기와 경사하강법 이전의 포스팅에서는 손실 함수와 수치 미분을 공부했습니다. 이번 포스팅에는 손실 함수의 기울기를 구하고 경사법으로 손실 함수 결과값이 최소가 되는 지점으로 가중치를 갱신시켜주는 방법에 대해 공부해보겠습니다. 4. 기울기 - Gradient 기울기는 모든 변수의 편미분을 벡터로 정리한 것을 의미합니다. $f$($x_0$, $x_1$) = $x_{0}^{2}$ + $x_{1}^{2}$ 이전의 포스팅에서는 $x_0$와 $x_1$의 편미분을 변수별로 따로 계산했습니다. 그럼 $x_0$와 $x_1$의 편미분을 동시에 계산하는 방법을 알아보겠습니다. 위 식에서 $x_0$ = 3, $x_1$ = 4 일때..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다. 신경망 학습 (1) - 손실 함수와 수치 미분 이번 포스팅의 주제는 신경망 학습입니다. 여기서 학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 뜻합니다. 손실 함수를 소개합니다. 손실 함수는 신경망이 학습할 수 있도록 해주는 지표입니다. 이 손실 함수의 결과값을 가장 작게 만드는 가중치 매개변수를 찾는 것이 학습의 목표입니다. 경사법을 소개합니다. 손실 함수의 값을 가급적 작게 만드는 기법으로, 함수의 기울기를 활용합니다. 1. 데이터에서 학습한다. 신경망의 특징은 데이터를 보고 학습할 수 있다는 점입니다. 데이터에서 학습한다는 것은 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 뜻입니다. 신경..