딥러닝 공부방

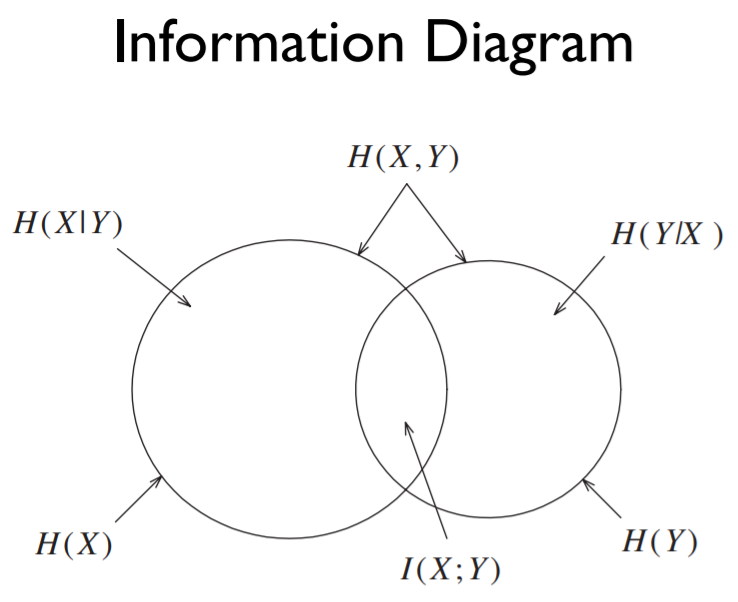
Chain Rule for Entropy 엔트로피에서도 연쇄 법칙이 성립합니다. 이전 포스팅에서의 entropy diagram을 생각해 보았을 때, H(1,2) = H(1) + H(2$\mid$1)은 당연합니다. Chain Rule for Conditional Entropy 조건부 엔트로피에 대해서도 연쇄 법칙이 성립합니다. Chain Rule for Mutual Information Chain Rule for Conditional Mutual Information 증명은 너무 어렵네요..ㅎㅎ 다른 증명입니다. 출처: Coursera Information Theory 강의 https://www.coursera.org/learn/information-theory/home/info Coursera | Onl..

서포트 벡터 분류기(Support Vector Classifiers) 위 그림 같은 경우에 training observation은 분리 초평면(separating hyperplane)에 의해 분류되지 않습니다. 이처럼 두 class에 속하는 관측치(observation)들이 항상 초평면에 의해 분류되는 것은 아닙니다. 또한 관측치가 하나 추가되면 위 그림처럼 초평면이 급격하게 변화될 수 있습니다. 마진이 급격하게 감소했는데 마진은 observation에 할당된 class의 확신을 의미하므로 문제가 발생할 수 있습니다. 이처럼 분리 초평면에 기반한 분류기는 하나의 개별 관측치에 민감하게 반응할 수 있습니다. 또한 과적합을 유발할 수 있습니다. 이 경우에 관측값들을 완벽하게 두 클래스로 분리하지 않는 초평면..

최대 마진 분류기(The Maximal Margin Classifier) 데이터를 초평면을 사용하여 완벽하게 분류할 수 있다면 무한개의 초평면이 존재할 것입니다. 초평면이 어느 관측치와도 만나지 않으면서 약간 위 아래로 움직일 수 있기 때문입니다. 분리 초평면을 사용한 분류기를 구성하기 위하여 어떤 초평면을 사용해야 할지 합리적인 방법이 있어야 합니다. training observation으로부터 가장 멀리 떨어진 분리 초평면(separating hyperplane)인 최대 마진 초평면(maximal margin hyperplane)을 선택하는 것이 자연스럽습니다. 즉, 주어진 분리 초평면 부터 각 training observation 까지의 수직 거리를 계산하고 가장 작은 거리를 마진(margin)이라..

Continuity of Shannon's Information Measuers for Fixed Finite Alphabets All Shannon's information measures are continuous when the alphabets are fixed and finite. For countable alphabets, Shannon's information measures are everywhere discontinuous 이번 내용에서 배우는 내용은 이 책의 범위에 벗어나지만 어느정도 이해를 해야합니다. finite alphabets와 countable alphabets 사이에 큰 차이점이 존재합니다. finite alphabets에서는 shannon's information measu..

부스팅(Boosting) 결정 트리의 예측을 향상시키는 또다른 방법은 부스팅(boosting) 입니다. 부트스트랩을 사용하여 다수의 training data 부분 집합을 생성하여 각 부분 집합에 대하여 각 트리를 적합하고 결과값을 평균하는 것이 배깅이었습니다. 각 트리는 부트스트랩 데이터셋을 기반으로 구축되고 트리는 서로 독립적입니다. 부스팅은 트리들이 순차적으로 만들어지는 것을 제외하고 이와 비슷한 방법으로 작동합니다. 각 트리는 이전에 만들어진 트리로부터 정보를 사용하여 만들어집니다. 부스팅은 부트스트랩 샘플링을 사용하지 않습니다. 대신에 각 트리를 original dtaset의 수정된 버전에 적합합니다. 우선 회귀 트리를 고려하겠습니다. bagging과 같이 부스팅은 많은 수의 결정 트리를 결합합니..

랜덤 포레스트(Random Forests) 랜덤 포레스트는 트리들의 상관성을 제거하는 방법(decorrelate)으로 bagged tree에 대해 성능 향상을 제공합니다. bagging을 수행하기 위하여 decision tree를 구축해야 합니다. decision tree를 구축할 때, 전체 p개의 변수들 중에서 무작위 m개의 변수들로 분할을 수행할 것인지 고려해야 합니다. 분할은 이 m개의 변수중 하나만을 사용하여 진행하고, 각 분할에서 새로운 m개의 변수를 추출합니다. 일반적으로 m = $\sqrt{q}$로 선정합니다. 예를 들어 p=13이면 m=4를 선택합니다. 다른 말로하면, random forest를 만드는 도중에 트리의 각 분할에서 알고리즘은 사용가능한 다수의 변수들을 고려하는 것이 허용되지 ..

배깅은 강력한 예측 모델을 구축하기위해 트리를 buidling block으로 사용합니다. 배깅(Bagging) 이전에 공부했었던 부트스트랩(bootstrap)은 관심있는 양의 표준 편차를 계산하기 어려운 상황에서 사용하는 강력한 아이디어 입니다. 이 부트스트랩을 결정트리와 같은 통계 방법 성능을 향상시키기 위해 완전히 다른 맥락으로 사용할 수 있습니다. 결정트리(decision tree)는 high variance가 문제 됩니다. 이는 학습 데이터를 무작위로 두 부분으로 분할하고 의사 결정 트리를 두 부분에 적합하면 두 결과가 상당히 다를 수 있다는 것을 의미합니다. 반면에 low variance는 서로 다른 데이터셋에 반복적으로 적합을 진행해도 동일한 결과를 생성하는 것을 의미합니다. 부트스트랩 통합(..

Shannon's Information Measures Shannon's information measure에는 4가지 유형이 있습니다. 1. entropy 2. conditional entropy 3. mutial information 4. conditional mutual information Entropy의 정의와 함께 시작하겠습니다. Entropy 컴퓨터 사이언스에서 bit와 정보 이론에서 bit는 다릅니다. 캄퓨터 사이언스에서 bit는 0과 1을 의미하고 정보이론에서는 랜덤 변수의 엔트로피가 bit로 측정됩니다. 엔트로피는 X의 분포만 의존합니다. X가 갖는 실제 값은 상관 없습니다. 다음 예제를 살펴보면 엔트로피는 분포에만 종속적이라는 것을 확인할 수 있습니다. Compact way to re..

트리와 선형모델 선형 회귀는 다음 형태의 모델을 가정합니다. 회귀 트리는 다음 형태의 모델을 가정합니다. 만약 반응 변수와 설명 변수 사이의 관계가 선형이라면 선형 모델이 더 좋은 성능을 갖습니다. 관계가 비선형인 경우에 트리가 더 좋은 성능을 갖습니다. 모델을 선택하는데에 정확도를 제외하고 해석력과 시각화를 고려할 수 있습니다. 트리의 경우 해석력과 시각화가 선형모델보다 뛰어납니다. 위 그림을 보면 데이터가 선형 관계인 경우에 선형 모델이 결정경계를 잘 형성하고, 데이터가 비선형 관계인 경우에 트리가 결정경계를 잘 형성합니다. 트리의 장단점 트리는 설명하기 쉽습니다. 선형 회귀보다 설명하기 더 쉽습니다. 의사결정트리가 다른 기법들보다 인간의 의사결정 과정을 더 밀접하게 반영합니다. 트리는 비전문가도 쉽..

분류 트리(Classification Tree) 분류 트리는 이전에 공부했었던 회귀 트리와 매우 유사하며 차이점은 양적 반응 변수가 아니라 질적 반응 변수를 예측한다는 것입니다. 회귀 트리는 관측값이 속한 terminal node의 평균값을 사용하여 예측했습니다. 이와 반대로 분류 트리는 관측치가 속하는 구역에서 훈련 관측치의 가방 빈번하게 발생하는 클래스에 관측치가 해당하는지를 예측합니다. 따라서 터미널 노드에 해당하는 클래스 예측값(class prediction) 뿐만 아니라 그 구역에 해당하는 훈련 관측치들의 클래스 비율(class proportion)에도 관심이 있습니다. 분류 트리를 구축하기 위해 회귀 트리와 마찬가지로 재귀 이진 분할을 사용합니다. 이진 분할을 위한 기준으로 RSS는 사용할 수..