딥러닝 공부방

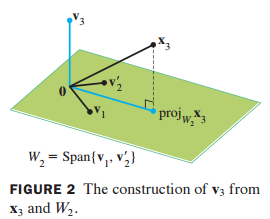
이번 포스팅에서는 그람슈미트 과정(Gram-Schmidt process)와 QR 분해(QR factorization)에 대해 공부해보겠습니다. 그람슈미트 과정은 임의의 부분공간(subspace)이 있을 때 그 subspace를 이루는 직교 기저(orthogonal basis)를 찾는 것입니다. 1. 그람슈미트 과정의 기본 아이디어(Basis idea for the Gram-Schmidt process) 2차원 공간 W = Span{$x_1, x_2$}라고 가정할 때, W에 대한 직교 기저(orthogonal basis) {$v_1, v_2$} 를 찾아보겠습니다. $v_1$ = $x_1$로 둡니다. 그리고 $v_2$는 $x_2$에서 $x_2$를 $x_1$에 projection 한 것을 빼주면 다음과 같이 ..

저번 포스팅에서 정사영이 무엇인지 간략하게 알아보았습니다. 이번에는 정사영에 대해 자세히 배워보도록 하겠습니다. 저번 시간에 배운 내용을 복습해보겠습니다. 벡터 y와 부분공간 W가 주어졌을 때, y를 서로 직교하는 두 개의 벡터 합으로 분해할 수 있다고 배웠습니다. 여기서 $\hat{y}$는 W 부분공간 안에 있으며 다음과 같이 구할 수 있습니다. 1. 이론 8 직교 분해 이론(The Orthogonal Decomposition Theorem) 벡터 y를 두 개의 벡터로 분해(decomposition)할 수 있으며 $\hat{y}$는 W 부분 공간안에 존재하고 z는 $W^{\perp}$에 존재합니다. 만약 {$u_1, ... ,u_p$}가 W의 직교 기저(orthogonal basis) 이면 $\hat{..

1. 직교 집합(Orthogonal Sets) 벡터의 집합 {$u_1, ... ,u_p$}이 존재할 때, 집합의 모든 벡터 쌍이 직교(orthogonal)이면 직교 집합이라고 합니다. 즉 $u_i\cdot u_j$ = 0 입니다. 직교 집합 {$u_1,u_2,u_3$}이 주어졌을 때, 각각의 벡터를 내적해보겠습니다. 이처럼 각각의 벡터 쌍의 내적은 0이 됩니다. 2. 이론 4 S가 non-zero 벡터들의 직교 집합이면 S는 선형 독립(linearly independent)이고, 직교 집합은 S를 span하는 기저(basis)입니다. 증명 S의 직교 집합의 선형 결합(linear combination)이 0이라고 가정하겠습니다. 양변에 $u_1$을 곱하겠습니다. 서로 다른 벡터의 내적은 직교이므로 0이 ..

이번 포스팅에서 내적(inner product), 길이(length), 직교성(orthogonality)에 대해 알아보도록 하겠습니다. 지금까지 Ax = b 형태의 방정식을 푸는 법을 배웠습니다. 하지만 실험 데이터로 수식을 세워 풀어보면 수식과 일치하는 경우가 거의 없습니다. 실험 데이터는 오차가 있을 수 밖에 없기 때문입니다. 이 경우에 b와 제일 가까이 있는 x를 찾아야 합니다. 이것이 제일 합리적인 방법입니다. 1. 내적(Inner Product) 직교성을 알아보기전에 먼저, 내적에 대해 알아보겠습니다. 동일한 $R^n$ 공간에서 두 개의 벡터가 주어졌습니다. u와 v의 내적은 다음과 같이 정의됩니다. 이는 $u^T$v를 의미합니다. 또한 두 벡터의 순서가 바뀌어도 됩니다. 두 벡터의 내적을 $u..

딥러닝 논문 읽고 파이토치로 구현하기 시리즈 1. [논문 리뷰] LeNet-5 (1998), 파이토치로 구현하기 이번에 읽어볼 논문은 'ImageNet Classification with Deep Convilutional Neural Networks'(AlexNet) 입니다. AlexNet 컴퓨터 비전 분야의 '올림픽'이라 할 수 있는 ILSVRC(ImageNet Large-Scale Visual Recognition Challenge)의 2012년 대회에서 AlexNet이 Top 5 test error 기준 15.4%를 기록해 2위(26.2%)를 큰 폭으로 따돌리고 1위를 차지했습니다. (Top 5 test error란 모델이 예측한 최상위 5개 범주 가운데 정답이 없는 경우의 오류율을 말합니다.) 이..

가장 기본적인 CNN 구조인 LeNet-5 논문을 읽어보고 파이토치로 직접 구현해보면서 CNN에 대한 이해도를 높여보겠습니다. LeNet-5은 1998년 Yann LeCun의 논문 'Gradient-Based Learning Applied to Document Recognition' 에 담겨있는 CNN 신경망의 구조를 의미합니다. 위 논문은 46page에 달하는 논문으로 문자 인식 업무에 CNN이 효과적인 이유에 대해 기술되어 있어, 읽어본다면 CNN에 대한 이해도를 높일 수 있을 것이라고 생각 합니다. 이제, 논문을 요약해보고 PyTorch로 구현해보겠습니다. 1. LeNet-5 등장 배경 LeNet-5은 Yann LeCun이 손으로 적힌 우편 번호를 전통적인 방법보다 효율적으로 확인하기 위해 고안된 ..

이번에 고유치가 복소수일 때 어떤 성질을 지니게 되는지 공부해보겠습니다. 1. 복소수 공간에서 행렬의 고유치-고유벡터 이론 - Matrix Eigenvalue-Eigenvector Theory for $C^n$ 이전까지 $R^n$ 공간에 있는 eigenvalues와 eigenvector에 대해 공부해보았습니다. 그러면 eigenvalues와 eigenvector가 $C^n$ 공간에 있는 경우에 어떻게 작용되는지 알아보겠습니다. $R^n$ space에 있는 이론이 그대로 적용되어 정의도 같습니다. 단지, eigenvalue가 complex value를 갖게 될 뿐입니다. 복소수 scalar $\lambda$가 det(A-$\lambda$I) = 0을 만족하면 Ax = $\lambda$x 에서 $C^n$ s..

LeetCode 771. Jewels and Stones - 보석과 돌 Jewels and Stones - LeetCode Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview. leetcode.com 문제 돌을 나타내는 S와 보석을 나타내는 J 가 주어졌을 때, 돌안에 보석이 몇개 들어있는지 알려주기 예시 풀이 1. 해시 테이블을 이용한 풀이 class Solution: def numJewelsInStones(self, J: str, S: str) -> int: freq = {} count = 0 for c..

터미널 창에서 깃을 사용하기 위해 쓰는 명령은 리눅스 명령과 같습니다. 깃을 사용하기 전에 미리 알아두어야 할 리눅스 명령을 먼저 살펴보겠습니다. 현재 디렉터리 살펴보기 깃 배시를 실행한 후 커서 윗줄을 보면 맨 끝에 물결 표시(~)가 있습니다. 현재 홈 디렉터리에 있다는 의미입니다. 1. pwd : 현재 위치의 경로 파악하기 pwd 명령어를 입력하면 현재 위치의 경로가 나타납니다. 2. ls : 현재 디렉터리에 어떤 파일이나 디렉터리가 있는지 확인하기 옵션을 추가하려면 붙임표(-)와 원하는 옵션을 나타내는 글자를 함께 입력합니다. ls -l : 파일과 디렉터리의 상세 정보까지 표시하는 옵션 ls -a : 숨긴 파일과 디렉터리를 표시하기 두 옵션을 함께 사용하려면 -la, -al 처럼 순서에 상관없이 글..

깃을 사용하기 위해서는 컴퓨터에 깃을 설치해야 합니다. 윈도우에 깃 설치하는 방법에 대해 알아보겠습니다. 윈도우에 깃 설치하기 깃에서는 리눅스 명령을 사용하기 때문에 윈도우에 깃을 설치하면 리눅스 명령을 사용할 수 있도록 깃 배시(Git Bash)라는 프로그램이 함께 설치됩니다. 1. 깃 홈페이지에서 깃 설치하기 git-scm.com/ Git git-scm.com 여기 홈페이지에서 Download를 누르면 설치가 진행됩니다. 2. 설치된 파일을 실행합니다. 기본 값 그대로 진행하여도 상관 없습니다. Next를 계속 눌러 진행하면 Git 설치가 완료됩니다. 기본값으로 진행하여도 상관없습니다. 3. 제대로 설치되었는지 확인하기 윈도우 검색 창에 git이라고 입력한 후 Git Bash를 실행시킵니다. 실행된 ..