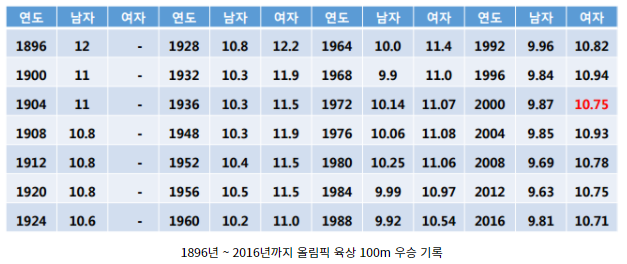
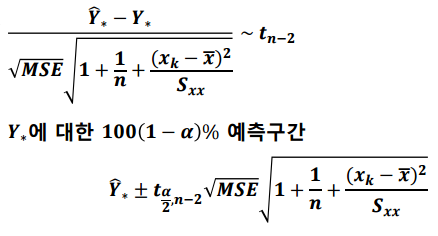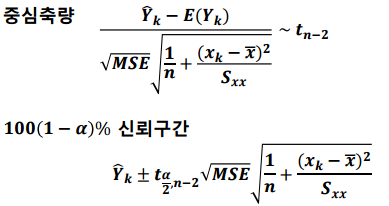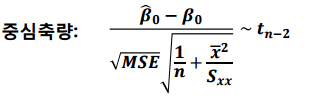여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 새로운 관측값에 대한 예측 새로운 설명변수(x)에 대한 예측값에 대한 추정과 예측구간을 알아보겠습니다. 저번 포스팅에서는 $x_k$일 때, $y_k$의 평균의 예측값을 공부했습니다. 평균의 예측값을 구할 때는 관심이 $b_0 + b_1x_k$에 관심이 있었지만 새로운 관측값에 대한 예측은 오차까지 고려한 $b_0 + b_1x_k + \epsilon_k$에 관심이 있습니다. 1. 새로운 $x_*$에 대한 예측값 $Y_*$의 추론 $\hat{Y_*}$에 관심이 있으면 $\hat{b_0} + \hat{b_1}x_*$를 이용해도 되지만 $\epsilon_*$에 관심이 있으면 예측오차 $\hat{Y_*} - Y_*$에 관심을 가져야 합..