딥러닝 공부방

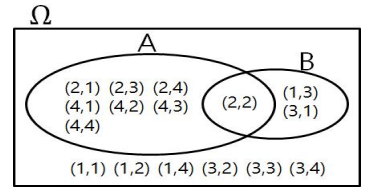
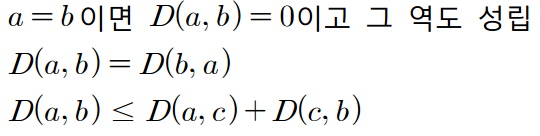(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다. 확률의 공리와 이를 기반으로 유도된 확률에 대한 기본 성질을 알아보겠습니다. 2.3 공리적 확률 공리란 증명할 수 없으나 옳다고 판단되는 명제입니다. 확률이론들은 확률의 공리를 토대로 만들어졌습니다. 표본공간상에서 아래의 공리를 만족하는 P()를 확률측도(probability measure)라고 하고 P(A)를 사건 A의 확률이라고 합니다. 확률의 공리에 대해서 알아보겠습니다. 확률의 공리 공리 1. P(Ω) = 1 공리 2. 사건 A $\subset$ Ω에 대해, 0 $\leq$ P(A) $\leq$ 1 공리 3. 서로배반인 사건 A와 B에 대해, P(AU..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다. 상대도수의 극한의 개념으로 이해하는 확률에 대해 알아보겠습니다. 이를 통해 확률이 모집단에 대한 것임을 이해해보겠습니다. 2.2 상대도수의 극한개념 (1) 통계적 확률(statistical probability) 통계적 확률이란 각각의 실험에서 발생하는 결과는 표본이고 실험을 무한히 반복한다는 것은 표본이 결국 모집단이 된다는 의미입니다. 결국, 확률은 모집단이 어떤 형태로 구성되어 있는지를 보여주게 됩니다. 동전의 앞면이 나올 사건을 A라고 하면 P(A) = 1/2입니다. 이는 앞면과 뒷면의 발생가능성이 동일하다고 가정하는 고전적 확률입니다. 동전 던지기 ..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다. 표본공간 및 사건의 원소 개수를 효율적으로 계산하는 기본 공식(경우의 수)을 소개하겠습니다. 경우의 수 - the number of cases 확률을 계산하기 위해 표본공간과 사건에 있는 원소의 개수를 효율적으로 계산하는 것이 중요합니다. 어떤 실험을 했을 때 발생할 수 있는 결과의 개수, 즉 원소의 개수를 경우의 수(the number of cases)라고 합니다. 경우의 수를 계산하는 데 있어 기본 법칙은 곱의 법칙(multiplication)입니다. 곱의 법칙에 의하면 어떤 실험이 m개의 연속된 단계로 이루어져 있고 $i$-번째 단계에서 발생 가능한 결..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다. 2. 확률의 이해 2.1 고전적 확률 고전적 확률(등확률)은 표본공간의 각 원소(근원사건)의 발생가능성이 동일(equally likely)한 확률을 의미합니다. 여기서 n은 표본공간의 원소개수, k는 사건 A의 원소개수를 의미합니다. 예를 들어, 정사면체 주사위 한 개를 던질 때 표본공간은 {1, 2, 3, 4, 5, 6}이 되며 원소 개수는 6이 됩니다. 각각의 사건이 발생할 확률은 1/6로 동일합니다. 연속표본공간(continous sample space) 구매한 스마트폰의 수명 측정한다고 가정했을 때 스마트폰의 수명(x)은 $0 \leq x$가 됩니다...

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다. 이번 포스팅에서는 확률을 정의하기 위한 전제조건을 알아보겠습니다. 또한 확률, 확률실험, 표본공간, 사건, 집합의 연산법칙, 벤다이어그램에 대해서 공부하겠습니다. 1. 확률 확률은 모집단1에서 표본을 뽑을 때 꼭 필요한 개념입니다. 어떠한 표본을 뽑는지에 따라 기술통계의 통계값(평균, 분산)이 달라지기 때문입니다. 이제 모집단1에서 표본을 생성하는 확률에 대해서 알아보겠습니다. 1.1 확률이란? 확률(probability)은 어떠한 사건이 발생할 가능성이 얼마나 되는지를 나타내는 [0, 1]의 수치적 측도입니다. 확률을 언급하기 위해서는 해당하는 확률실험(r..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다. 표나 그래프를 이용하여 수치자료를 그룹별로 나누어 비교하는 방법을 알아보겠습니다. 두 수치자료의 관계를 나타내거나 하나는 범주형, 하나는 수치형 자료를 이용하는 표나 그래프를 알아보겠습니다. 4. 비교그림 (1) 표를 이용한 비교 자료구조와 분석목적에 따라 목적에 맞는 표를 만들 수 있습니다. 구조로는 분류자료(그룹, 범주) + 수치자료로 구성되어 있는 표를 알아보겠습니다. 목적으로는 그룹 간 비교입니다. 이를 위해 수치자료의 특성을 나타내는 값을 그룹별로 정리하여야 합니다. 예를 들어 표본크기, 평균, 표준편차 등으로 그룹을 나누는 경우가 있습니다. 이를 정당별 당선자 ..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다. 자료의 분표 형태가 대칭인지 아닌지를 나타내는 통계값(왜도)을 알아보겠습니다. 분포의 꼬리 부분이 얼마나 두터운지를 나타내는 통계값(첨도)를 알아보겠습니다. 7.3 분포의 형태 지금까지의 포스팅에서는 자료의 중심위치와 산포에 관련된 통계값에 대해 알아보았습니다. 수치형 자료에 대한 통계분석방법에서는 대부분 모집단의 형태가 중심위치를 기준으로 좌우대칭인 것으로 가정하고 있습니다. 분석방법의 적절성은 가정한 조건을 자료가 얼마나 만족하고 있는지에 따라 영향을 받습니다. 이런 점에서 자료가 어떤 형태로 분포되어 있는지, 자료가 모집단의 가정을 만족하는지 확인하는 통계값에 대해 ..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다. 자료들 간의 거리를 이용하여 산포도를 계산하는 방법(표본분산, 표본표준편차)을 알아보겠습니다. 자료분석에서 측정 단위에 영향을 받지 않게 만드는 표준화에 대해 알아보겠습니다. 그리고 평균으로 표본표준편차를 보정한 변동계수를 알아보겠습니다. (3) 표본분산과 표본표준편차 범위나 사분위수범위의 경우 특정 위치의 두 값을 이용하기 때문에 표본의 정보를 많이 활용하지 못합니다. 이런 문제를 해결하기 위해 모든 자료들 간의 거리의 합을 이용하는 것 입니다. 수학적으로 거리 $D$는 임의의 점 a, b, c에 대해 다음과 같은 성질을 만족합니다. 우리는 거리$D$의 성질 중 $D$(..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다. 평균이 갖고 있는 단점은 이상점에 민감하다(이상점에 로보스트하지 않다)는 것이었습니다. 평균이 갖고 있는 단점을 해결할 수 있는 대체 통계값을 계산하는 방법(중앙값, 절사평균, 최빈값)과 성질을 알아보겠습니다. (6) 표본중앙값(sample median, 표본중위수) 표본중앙값은 자료를 크기순서대로 나열했을 때 가운데 위치에 있는 값으로 표본중위수라고도 합니다. 표본을 오름차순으로 정렬한 것을 순서통계량(order statistics)라고 합니다. ($x_1 < x_2 < ... < x_n$) 표본중앙값을 일반식으로 나타내면 다음과 같습니다. 여기서 $k_1 = (n+1)..

(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다. (k-mooc 통계학의 이해1, 여인권)을 수강하면서 정리해보았습니다. 수치자료를 범주화하는 방법을 알아보겠습니다. 또, 범주화된 수치자료를 표나 그래프를 이용하여 정리하는 방법을 알아보겠습니다. 4. 표를 이용한 정리(수치형) 4.1 도수분포표 - frequency table 수치자료에 대한 도수분포표를 만들 때에는 관측된 값들을 몇 개의 구간으로 범주화하여 해당 그룹에 속한 관측개체의 빈도로 도수분포표를 만듭니다. 우선, 수치자료의 범주화를 알아보겠습니다. 수치자료를 범주화할 때는 몇 개의 범주로 나눌 것인지와 범주의 경계값을 얼마로 할 것인지 정해야 합니다. 자료의 특성을 고려해 분석자가 임의대로 결정할 수 있습니다. 계급(class) ..