딥러닝 공부방

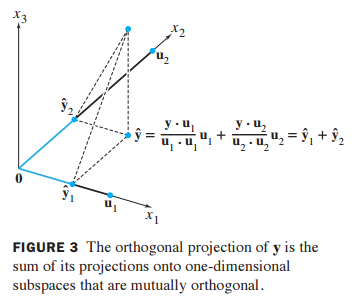
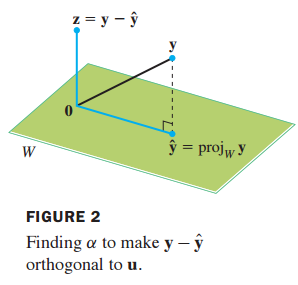
저번 포스팅에서 정사영이 무엇인지 간략하게 알아보았습니다. 이번에는 정사영에 대해 자세히 배워보도록 하겠습니다. 저번 시간에 배운 내용을 복습해보겠습니다. 벡터 y와 부분공간 W가 주어졌을 때, y를 서로 직교하는 두 개의 벡터 합으로 분해할 수 있다고 배웠습니다. 여기서 $\hat{y}$는 W 부분공간 안에 있으며 다음과 같이 구할 수 있습니다. 1. 이론 8 직교 분해 이론(The Orthogonal Decomposition Theorem) 벡터 y를 두 개의 벡터로 분해(decomposition)할 수 있으며 $\hat{y}$는 W 부분 공간안에 존재하고 z는 $W^{\perp}$에 존재합니다. 만약 {$u_1, ... ,u_p$}가 W의 직교 기저(orthogonal basis) 이면 $\hat{..

1. 직교 집합(Orthogonal Sets) 벡터의 집합 {$u_1, ... ,u_p$}이 존재할 때, 집합의 모든 벡터 쌍이 직교(orthogonal)이면 직교 집합이라고 합니다. 즉 $u_i\cdot u_j$ = 0 입니다. 직교 집합 {$u_1,u_2,u_3$}이 주어졌을 때, 각각의 벡터를 내적해보겠습니다. 이처럼 각각의 벡터 쌍의 내적은 0이 됩니다. 2. 이론 4 S가 non-zero 벡터들의 직교 집합이면 S는 선형 독립(linearly independent)이고, 직교 집합은 S를 span하는 기저(basis)입니다. 증명 S의 직교 집합의 선형 결합(linear combination)이 0이라고 가정하겠습니다. 양변에 $u_1$을 곱하겠습니다. 서로 다른 벡터의 내적은 직교이므로 0이 ..

이번 포스팅에서 내적(inner product), 길이(length), 직교성(orthogonality)에 대해 알아보도록 하겠습니다. 지금까지 Ax = b 형태의 방정식을 푸는 법을 배웠습니다. 하지만 실험 데이터로 수식을 세워 풀어보면 수식과 일치하는 경우가 거의 없습니다. 실험 데이터는 오차가 있을 수 밖에 없기 때문입니다. 이 경우에 b와 제일 가까이 있는 x를 찾아야 합니다. 이것이 제일 합리적인 방법입니다. 1. 내적(Inner Product) 직교성을 알아보기전에 먼저, 내적에 대해 알아보겠습니다. 동일한 $R^n$ 공간에서 두 개의 벡터가 주어졌습니다. u와 v의 내적은 다음과 같이 정의됩니다. 이는 $u^T$v를 의미합니다. 또한 두 벡터의 순서가 바뀌어도 됩니다. 두 벡터의 내적을 $u..

이번에 고유치가 복소수일 때 어떤 성질을 지니게 되는지 공부해보겠습니다. 1. 복소수 공간에서 행렬의 고유치-고유벡터 이론 - Matrix Eigenvalue-Eigenvector Theory for $C^n$ 이전까지 $R^n$ 공간에 있는 eigenvalues와 eigenvector에 대해 공부해보았습니다. 그러면 eigenvalues와 eigenvector가 $C^n$ 공간에 있는 경우에 어떻게 작용되는지 알아보겠습니다. $R^n$ space에 있는 이론이 그대로 적용되어 정의도 같습니다. 단지, eigenvalue가 complex value를 갖게 될 뿐입니다. 복소수 scalar $\lambda$가 det(A-$\lambda$I) = 0을 만족하면 Ax = $\lambda$x 에서 $C^n$ s..

이번에 공부해볼 내용은 고유벡터와 선형변환의 관계입니다. 1. 선형 변환의 행렬 - The matrix of Linear Transformation V가 n-dimensional vector space이고 W는 m-dimensional vector space로 주어졌을 때 V와 W를 연결시켜주는 T linear transformation을 가정하겠습니다.. 그러면 B basis로 표현되는 x의 coordinate vector $[x]_B$와 C basis로 표현되는 T(x)의 coordinate vector $[T(x)]_C$를 연결시키는 행렬이 있는지에 대한 궁금증이 생깁니다. $[x]_B$와 $[T(x)]_C$ 사이의 연결은 쉽게 찾을 수 있습니다. V에 대한 basis B가 {$b_1, ... ,b..

이번 포스팅에서 공부할 내용은 대각화(Diagonalization)입니다. 1. 대각화(Diagonalization) 정사각행렬(square matrix) A가 대각 행렬(diagonal matrix)와 유사(similar)하면 A를 대각화가능(diagonalizable)하다고 합니다. 즉, A = PD$P^{-1}$ 일 때 A가 diagobalizable이라고 합니다. 예시 문제 1 diagonal matrix의 squre은 diagonal term의 squre입니다. 만약 A가 D와 similar하면 $A^k$를 쉽게 계산할 수 있습니다. 예시 문제 2 A가 diagonalizable할 때, $A^k$를 구하는 문제입니다. 2. 이론 4. 대각화 이론 - Theorem 4. The Diagonaliz..

이번 포스팅에서 특성 방정식(Characteristic equation)에 대해 알아보겠습니다. characteristic equation은 eigenvalue와 밀접한 관련이 있는 equation입니다. 저번 포스팅에서 공부했던 것을 복습하자면 주어진 A 행렬의 eigen value를 구할 때 (A - $\lambda$I)x = 0 을 이용합니다. A가 eigen value를 갖고 있으려면 Ax=0에서 nontrivial solution을 갖고 있어야 합니다. 이는 A가 not invertible을 의미하고 det(A) = 0이 되어야 합니다. 이를 통해 eigenvalue는 3,7 인것을 확인할 수 있습니다. 1. 특성 방정식 - The Characteristic Equation characteris..

이번 포스팅에서는 고유벡터와 고유값에 대해 알아보겠습니다. 고유값 - eigenvalue 고유벡터 - eigenvector 고유공간 - eigenspace 1. 고유값과 고유벡터의 기본 아이디어 행렬 A, u, v가 다음과 같이 주어졌을 때 곱셈 결과를 시각적으로 표현해 보겠습니다. Av의 결과는 동일한 line에 solution이 존재하도록 결과가 나왔습니다. 이것이 Eigenvalue와 Eigenvector의 기본 idea입니다. 2. 고유벡터 - Eigenvector 고유벡터를 정의하면 다음과 같습니다. Ax = $\lambda$x를 만족하는 nonzero vector x가 eigenvector입니다. 또한, Ax = $\lambda$x에서 x가 nontrivial solution이 존재할 때 sc..

이번 포스팅에서 공부할 내용은 다음과 같습니다. 크라메이 법칙 - Cramer's Rule 역행렬 공식 - Inverse formula 면적과 부피에서 행렬식 - Determinants as area and volumn 선형 변환 - Linear transformation 1. 크라메이 법칙 - Cramer's Rule Cramer's Rule을 사용하기 위해서는 새로운 정의가 필요합니다. A의 i th column을 b로 치환한 것을 $A_i(b)$로 표현하겠습니다. 2. 이론 7. 크라메이 법칙 - Theorem 7. Cramer's Rule A가 n x n 크기의 invertible 행렬일 때 Ax=b의 해는 다음과 같이 구할 수 있습니다. $A_i(b)$는 A행렬의 i th culumn을 b로 치..

이번 포스팅에서 배울 내용은 행 연산에 의한 행렬식 변화 - Determinant changes by row operations det $\neq$ 0 det $A^T$ = det A det AB = (det A)(det B) 입니다. 1. 이론 3. 행 연산 - Theorem 3. Row Operations a. A의 하나의 row 곱이 다른 row에 더해져 B 행렬이 만들어지면 det B = det A 입니다. 이는 row replacement를 의미합니다. b. B를 만드기 위해 A의 두개의 row가 interchange 됬으면 det B = -det A 입니다. c. A의 하나의 row에 k가 곱해져 B가 만들어졌으면 det B = k det A 입니다. scaling을 의미합니다. 이 세가지 성..